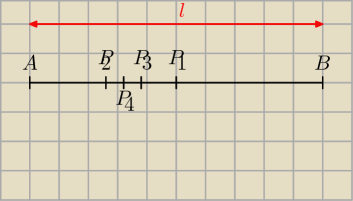
Granice Tomek.Noah: Punk P₁ dzieli odcinek AB o długosc l na dwie rowne czesci,punkt P₂ dzieli odcinek AP₁ na polowy, Punkt P₃ dzieli odcinek P₂P₁ na polowy, punkt P₄ w ten sam sposob dzieli odcienk P₂P₃ itd. Okreslic graniczne polozenie punktu P_n przy n→∞

	1
mi wyszlo ze wynosi ono		l moze ktos to sprawdzic?
	3

Jack: mi też

Tomek.Noah: hmm po Twoim komentarzu domyslam sie ze chcesz bym umiescil swoje rozwiazanie?

Jack: war. początkowe: a₀=0

	a
a1=
	2

war. "rekurencyjny"

	an−1+an−2
an=
	2

Gdzie n − to "n"−ty punkt, "a" to długość odcinka ("L" zamieniam na "a" żeby lepiej było widać) 2a_n=a_n−1+a_n−2 Zamieniam na równanie char−czne. 2λ²−λ−1=0

	1
λ1=1 oraz λ2=−
	2

Zatem postać rozwiązania: b_n=A(λ₁)ⁿ+B(λ₂)ⁿ Dla war. początkowych: b₀=A+B=0

	1		a
b1=A−		B=
	2		2

	3		a		a		a
Stąd		B=−		⇒ B=−		. Zatem A=		.
	2		2		3		3

	a		a		1		a		a
Ostatecznie: an=		−		(−		)n. Przy n→∞ mamy a∞=		+0=
	3		3		2		3		3

Jack: a nie! Zaskoczenie ale faktycznie pomyślałem o tym

Tomek.Noah:

	1
P1−		l
	2

	1
P2−		l
	4

	1
P3−		l
	8

. . .

	1
Pn=(		)nl
	2

	1
AP1=		l
	2

	1
AP2=		l
	4

AP₃=AP₂+P₃ . . . AP_n=AP_n−1+P_n AP_n−1=P₂+P₄+P₆+P₈+..+P_n−1 (parzyste bo jak sie wpatrzyc w orbazek widac ze dla nieparzystych mamy dlugsoc wieksza od AP_n )

	l(1−(1/4)n)
APn−1=
	3

	1
limAPn=		l
	3

n→∞

Tomek.Noah: Jack ja ejszcze nie studiuje narazie robie tak o zadani zeby zwiekszyc sztuke koncentracji a czy moje roz. jest poprawne?

Jack: co to jest to:

	1
P1−		l
	2

	1
P2−		l
	4

... itd? Jak to ma się do rysunku? Te działania sugerują że coś tu się zwiększa, tymczasem punkty "oscylują" wokół pewnej granicznej wartości

Tomek.Noah: znaczy sie ta − "odpowiada" taki nie logiczny szkic W poleceniu jest napisane by okreslic graniczne polozenie przyjalem wzgledem punktu A liczac odleglsoc co daje nam w sumie to samo... chyba

Jack: ok, przystępuję do kolejnej próby interpretacji

Tomek.Noah: wg mnie grunt to to ze wynik sie zgadza hehe

Jack:

	1
Twoje oznaczenie jednak nie jest ok. Zobacz, że przy P3 nie mamy		bo wyraźnie punkt ten
	8

	1
wyznacza dłuższy odcinek niż P2=		... Dokładnie rzecz biorąc to jest tak:
	4

	P2+P1
P3=		To stanowi u mnie właśnie warunek rekurencyjny
	2

Tomek.Noah:

	1
P3 daje nam polowe P2P1 co co jest		l
	4

	1		1
zatem jesli daje nam polowe P3−		P1P2 a to nam daje P3−		l (przypominam
	2		8

"−" odpowiada albo poprostu dzieli)

Jack: Ok, ciężko mi przebrnąć przez te oznaczenia... Jeszce raz spróbuję

Jack: nie dam dziś rady... niech ktoś spojrzy ^^

Tomek.Noah: hehe dobrze jest

Jack: mozliwe, bo podstawiając liczby za n dostaję te same liczby co u siebie Ale idei nie mogę zrozumieć (jakiś niedzisiejszy jestem)

Tomek.Noah: ja zazwyczaj mam nie konwencjonalne rozwazania moze daltego

Jack: mozliwe... To by wiele tłumaczyło z tego co się ze mną dzieje, gdy analizuję to rozwiązanie