i tak tego nie widać:( ICSP: Nie wie jak sie nazywa oś z? Wiem że oś x to oś odciętych oś y to oś rzędnych

Trivial: http://pl.wikipedia.org/wiki/O%C5%9B_wsp%C3%B3%C5%82rz%C4%99dnych

Jack: nie ośmieliłeś się podać nazwy?

ICSP: kto tą nazwę wymyślił? Oraz następne pytanko: Co prawdopodobnie będę miał na 1 roku matematyki?

ICSP: Chyba w końcu otworzę zbiór który kupiłem we wrześniu i zrobię trochę zadanek

Jack: analizę, algebrę, logikę itp − jak poszukasz na pewno znajdziesz plan zajęć na jakimś wydziale matematycznym

Trivial: Jack, masz rację, nie ośmieliłbym się podać tej nazwy. ICSP, tak jak mówi Jack. Analiza i algebra to pewniak, logika może trochę mniej (ja miałem 1 wykład).

ICSP: chce się komuś policzyć tg15^o? Ja policzyłem ale nie jestem pewien wyniku.

Trivial: 2−√3.

ICSP: czyli dobrze policzyłem

ICSP: To jak chcecie mogę wam dać jeszcze jedno zadanko

Trivial: Na co?

ICSP: planimetria

Trivial: Eh, planimetria... Tak w ogóle to na co idziesz?

ICSP: Matematyka na umcs

Trivial: To widzę Lublin. <:

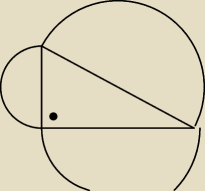
ICSP: Nie śmiać się z rysunku Suma pól tych półkoli jest 10 razy większa od pola trójkąta. Oblicz sumę tangensów kątów ostrych tego trójkąta.

ICSP: Tak lublin

Trivial: Oznaczając boki klasycznie jako a,b,c a pola półkoli przy odpowiednich bokach jako P_a, P_b i P_c i przy oznaczeniu pola trójkąta jako P mamy: P_a + P_b + P_c = 10*P

	a		1
Pa = π(		)2 =		πa2 itd.
	2		4

1		1
	π(a2 + b2 + c2) = 10*		ab
4		2

1
	π(a2 + b2) = 5ab
2

	10
a2 + b2 =		ab /: ab
	π

a		b		10
	+		=
b		a		π

	10
tgα + tgβ =		.
	π

ICSP: to liczymy pole całego koła czy tylko półkola?

Trivial:

	1
Oj no tak, trzeba razy		jeszcze.
	2

Trivial:

	20
Czyli wynik		.
	π

ICSP: brawo

Trivial: btw jaki zbiór?

ziomek: ja bym Ci polecił pobawić się z jednym z lepszych zbiorów ,trudniejszych od Krysickiego. Gorąco polecam Analizę matematyczną Banaś,Wędrychowicz wydawnictwo naukowo techniczne (WNT). Tam znajdziesz naprawdę dużo różnych zadań. poza tym: Z.Hellwig − Elementy Rachunku Prawdopodobienstwa i Statystyki Matematycznej Algebra Liniowa − T. Jurlewicz S.Lanowy, F.Przybylak, B.Szlek − Równania Różniczkowe. oraz bodajże zbiór z całkami itd Frizelhofa czy jakoś tak. (Dość trudny) Tylko trochę ciężko go nabyć.

ICSP: nie wiem. Nie myślałem jeszcze nad tym.

Basia: Zbiór zdań z analizy dla studentów matematyki z czasów gdy pochodne i całki były w szkole średniej, z piekielnie trudnymi zadaniami szczególnie z zakresu szeregów i równań różniczkowych to stary Demidowicz (tytułu nie pamiętam). W moich studenckich czasach tłumaczenia nie było, ale zadań tekstowych tam nie ma więc wystarczała szczątkowa znajomość rosyjskiego.