ciągi Ania:

	3
ciąg (an) określony jest wzorem an=		. Zbadaj monotoniczność tego ciągu i
	n2−15n+57

wyznacz największy wyraz ciągu (a_n)

rumpek: Jako iż nie chce mi się pisać obliczeń to powiem tyle że liczysz:

	3		3
an + 1 − an =		−		= [...]
	(n + 1)2 − 15(n + 1) + 57		n2 − 15n + 57

Już gdzieś robiłem to zadanie na tym forum bodajże, i chyba wyjdzie ciąg malejący, a jak malejący to największy wyraz będzie dla a₁ co trzeba będzie obliczyć. Dobranoc

Jack: najprawdopodobniej nie będzie w ogóle monotoniczny, ponieważ w mianowniku jest "parabola"... Żeby policzyć max wyraz całego ciągu a_n, należy policzyć... najmniejszy wyraz jaki może być w mianowniku, czyli wyznaczyć wierzchołek paraboli. Jeśli wyjdzie nienaturalna n₀, to szukaj dla [n₀]+1 (część całkowita z n₀) oraz [n₀]−1 (podobnie jak poprzednio) i weź tę dla której wartość będzie większa.

Jack: jeszcze co do monotoniczności: należy wyprowadzić wnioski analizując wierzchołek paraboli.

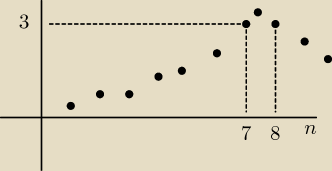
AS: Rośnie dla n = 1,2...7 Maleje dla n = 8,9,10,... Największa wartość dla n = 7 i n =8 ,Wynosi ona 3

AS: Dodatek Oczywiście kropka między 7 i 8 jest niepotrzebna. Zaznaczyłem tak z rozpędu.

Ania: AS a wyjaśnisz jak to zrobiłeś?

Ania: rumpek

	3		3
zrobiłam an+1 − an =		−		i co dalej sprowadzać do
	n2−13n+13		n2−15n+27

wspólnego mianownika?

AS: Wcale nie liczyłem,wrzuciłem do komputera,wykonałem wykres odpowiednim programem i odczytałem wyniki. Jak znajdę trochę czasu to policzę.

Ania:

	3		3
a{n+1−an=		−
	n2−13n+43		n2−15n+57

dla mianowników policzyłam deltę i w obu przypadkach wychodzi ujemna

Ania: Ze wskazówek Jack'a wyznaczyłam największy wyraz ciągu−czy Ktoś może sprawdzić czy dobrze? Najpierw dla paraboli liczę współrzędną p wierzchołka n²−15n+57=0

	b
p=−
	2a

	15
p=
	2

teraz podstawiam do wzoru ciągu

	3		2
anmax=		=
	15   2		5

Basia: jeżeli już koniecznie chcesz liczyć a_n+1 − a_n (a wcale nie musisz; As już wykazał, że ten ciąg nie jest monotoniczny) to:

	3(n2−15n+57) − 3(n2−13n+43)
an+1−an =
	(n2−13n+43)(n2−15n+57)

policzyłaś już Δ, wyszła Ci ujemna, więc wiesz, że n²−13n+43 > 0 zawsze i n²−15n+57 >0 zawsze zajmujesz się wobec tego tylkoi licznikiem L = 3n²−45n+171−3n²+39n−129 = −6n+42 −6n+42 > 0 −6n> −42 n < 7 −6n+42<0 −6n< −42 n>7 licznik jest czasem ujemny, a czasem dodatni czyli ciąg nie jest monotoniczny

Basia: p = ¹⁵₂ ∉N nie możesz tego podstawić do wzoru ciągu bierzesz n=7 i n=8 a₇ i a₈ będą największymi wyrazami tego ciągu stąd wniosek, że a₁,a₂,...,a₆ < a₇=a₈ > a₉, a₁₀,..... czyli ciąg nie jest monotoniczny

Ania: Basiu po raz kolejny rozjaśniasz mi zadanie DZIĘKUJĘ CI BARDZO!

Franek: Przepraszam za odświeżenie, ale mam wątpliwość co do tego zadania. Dlaczego szukając największego wyrazu bierzemy pod uwagę wierzchołek paraboli o wzorze n²−15n+57, a nie np. tej drugiej (n²−13n+43). Potrafi mi ktoś to wyjaśnić?

seba 1994: ciąg (an) określony jest wzorem an=n2−10n+16.wyznacz wszystkie ujemne wyrazy tego ciągu

ICSP: a_n = n² − 10n + 16 wyznaczyć wszystkie ujemne wyrazy − rozwiązać nierówność a_n < 0 a_n < 0 ⇒ n² − 10n + 16 < 0 dalej już sobie poradzisz.

bezendu: n²−10n+16<0 dokończ