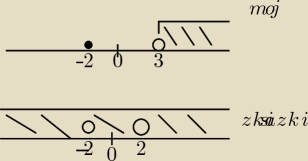
wyznacz zbiór Ania: Aby wyznaczyc zbiór tych liczb rzeczywistych, które spełniają formę zdaniową x−1<0 ⇒ (x+3)(x−5) =0 możemy postąpić nastepująco:, tutaj jest przykład itd. a) x² − 4 = 0 ⇒ x≥ 3 wynik zamieszcam na rysunkus prosze o wytłumaczenie moich blędów

krystek: Aniu, czy chodzi Tobie o x−1<0 i (x+3)(x−5)=0 czy o a) Jeżeli o a) to spełniaja x należące do przedziału <3;∞)

krystek: x²−4=0 to (x+2)(x−2)=0 to x=2lub x=−2

ziomek: inny punkt widzenia: ten znak ⇒ to implikacja implikacja jest zdaniem fałszywym jeśli z prawdy wynika fałsz (poprzednik jest prawdziwy, a następnik fałszywy). Poprzednik jest prawdziwy dla liczb −2 i 2, dla pozostałych wartości będzie fałszywy, więc formę zdaniową spełniają liczby rzeczywiste z wyjątkiem 2 i −2. (puste kółeczka na osi liczbowej) implikacja będzie prawdziwa.

ziomek: p q p⇒q 0 0 1 0 1 1 1 0 0 1 1 1

Ania: Rozumiem, Dzięki wielkie