druga pochodna z e tom21: witam, jak policzyć drugą pochodną z x2*e1/x pierwsza mi wyszła : e1/x*(2x−1) a drugą nie wiem jak policzyć, wychodzą jakieś skomplikowane rzeczy...

tom21: Poprawione żeby lepiej czytelne było witam, jak policzyć drugą pochodną z x²*e^1/x pierwsza mi wyszła : e^1/x*(2x−1) a drugą nie wiem jak policzyć, wychodzą jakieś skomplikowane rzeczy...

pochodna: (e^1/x−1/x²)(2x−1)+e^1/x*2

pochodna: 2xe^1/x−e^1/x−2/x+1/x²+2e^1_x

tom21: hmm, no ok, to mi chyba tak samo wyszło. Ale mam takie zadanie : Oblicz extremum lokalne funkcji x²*e^1/x więc liczę pierwszą pochodną wychodzi mi e^1/x*(2x−1), przyrównuję ją do 0 i x=1/2. co dalej ? W innych przypadkach wiem że oblicza się drugą pochodną i potem do niej wstawia x1 x2 i odczytuje czy ma minimum czy maximum. a tutaj jak ?

eleonor: podbijam!

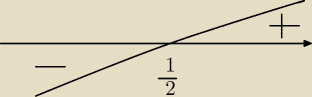
Nienor: Rysujesz rozwiązanie nierówności:

	1
√e(2x−1)>0 ⇔ 2x>1 ⇔ x>
	2

	1
W x=		pochodna zmienie znak, więc z warunku wyatrczającego na istnienie ekstremum (który
	2

	1
z kolei wynika z tw. Lagrange'a o przyrostach skończonych) x=		jest ekstremum lokalnym
	2

funkcji f(x). Dokładniej minimum lokalnym.

eleonor: a z jakbym chciała z drugiej pochodnej obliczyć punkty przegięcia, wklęsłość i wypukłość bo dochodzę do momentu w którym w drugiej pochodnej wychodzi mi x(2x²e¹/x + x^e1/x − 2) = 0