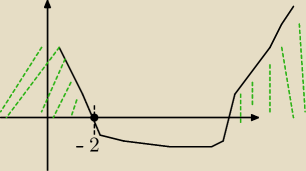
PROblem TOmek: Znajdź te wartości parametru m, dla których liczba 2 nie należy do zbioru rozwiązań nierówności x²+(m³+3)x−6m²−18m+44>0 −−−−−−−−−−−−−−−−−−−−−−−−− a>0 ramiona skierowane ku górze , więc funkcja powinna wyglądac (patrz. rysnek) dla mnie powinno być f(2)<0 ,a jak patrze na rozwiązanie to jest ,ze f(2)≤0. Nie czaje tego. przeciez jak 2 będzie zamknięte. to 2 bedzie rozwiązaniem tej nierówności..

rumpek: Która strona w kiełbasie?

TOmek: 60 już wiem, przeciez Δ musi byc większa od zera..dlatego f(2)=0 może być.

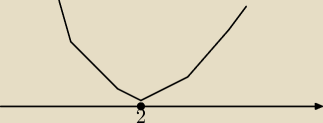
TOmek: chociaż, przecież moze tez byc sytuacja , gdy nadal nie wiem dlaczego f(2)≤0

rumpek: Przecież masz rozwiązanie do tego w kiełbasie, skoro dwójka nie spełnia nierówności f(x) > 0, to znaczy że spełnia nierówność f(2) ≤ 0 albo w drugą stronę. "Znajdź te wartości parametru m, dla których liczba 2 nie należy do zbioru rozwiązań nierówności x²+(m³+3)x−6m²−18m+44≥0" to warunek byłby f(2) < 0

TOmek: aha, czaje Dzieki

rumpek: Daj już spokój zadaniom z parametrem bierz się na trygonometrię

rumpek: za* trygonometrię

TOmek: trygonometrie juz zrobiłem, teraz mecze parametr

rumpek:

	2k2 − 1
Ustal liczby dla których równanie sin3x =		ma rozwiązanie
	k2 + 1

rumpek: Banalne takie odpowiedzi nie mam bo wymyślone na poczekaniu.

TOmek: i co ja mam to zrobić trygonometrie mam obcykaną tylko dla prostych równań i rysowaniu wykresów... mi nie potrzebna wiecej

rumpek: Nom zrób banał to napisz chociaż jakbyś to zrobił bo to najważniejsze A skoro tylko proste równania i rysowanie wykresów to po co robisz takie zadania z parametrami? Takich na pewno nie będzie na maturze

TOmek: sin3x <−1,1> więc

	2k2−1
−1≤		≤1 rozwiązujemy i gitara, ta?
	k2+1

TOmek: proste równania, moze źle to określiłem ,chociaz mi o ten typ zadania, wiesz na pewnie ocb. bo jest co roku nieustannie

rumpek: tak, a takie coś:

	k3 + k
cos27x =
	k − 2

rumpek: Bardzo proste są te zadania co Tobie pisze fajnie aby takie były na maturce

TOmek: czyli doby pomysl rozwiązania dałem w tym poprzednim

TOmek: nie zauwazyłem "tak"

rumpek: Niom − pisałem banalne

TOmek: kwadrat oznacza ,ze funkcja będzie tylko nad osią "x" i moze takze stykac oś x, 7x nic nam nie zmienia

	k3+k
czyli 0≤		≤2
	k−2

rumpek:

TOmek: 0≤bla≤1 tak?

rumpek: Nom, uważaj na to

TOmek: tak sobie pomyślałem <−1,1> czyli 2 jednostki

rumpek: 2 jednostki

TOmek: nie wiem jak to sie nazywa profesjonalnie , amplituda : )

rumpek: "tak sobie pomyślałem <−1,1> czyli 2 jednostki" − ty to przesuwałeś?

TOmek: nie po prostu sobie tak wyobraziłem, funkcje ,zeby była tylko dodatnia i pomyślałem ,jaki wtedy będzie zbiór wartosci, niestety 0≤blabla≤2 było błędne, dobra nie chce sie tłumaczyć, róbmy zadania

rumpek: sinx ∊ <−1,1> sin²x ∊ <0,1> Więc zbiór <−1,1> podniesiony do kwadratu jaki będzie miał zbiór?

	1		1
(−1)2 = 1 (−		)2 =		...
	2		4

Więc dlatego <0,1>

TOmek: ok