pytanie tn: w jaki sposób udowadniać tożsamości, w których niektóre funkcje trygonometryczne mają kąt α,a niektóre 2α

rumpek: Masz jakąś pod ręką?

ICSP: tak samo jak każde inne. np. Mamy udowdnić tożsamość sin2α = (sinα + cosα)² − 1 z lewej strony postarajmy się dotrzeć do prawej sin2α = 2sinαcosα = 1 + 2sinαcosα − 1 = sin²α + 2sinαcosα + cos²α − 1 = (sinα + cosα)² −1 = P reguła się nie zmienia. Trzeba znać tylko wzoru

tn: skąd wiesz że sin2α = 2sinαcosα w ogóle czy sinα jest równe sinαcosα?

rumpek: sin(α + α) = sinαcosα + cosαsinα = sinαcosα + sinαcosα = 2sinαcosα Stąd wie

Godzio: rumpek, a skąd wiesz że: sin(α + β) = sinαcosβ + sinβcosα ?

rumpek: W sensie 2sinαcosα pokazałem jak wyprowadzić, bo pytał Korzystając z sin(α + β) które również można wyprowadzić

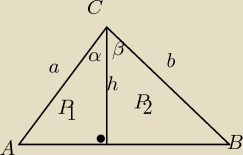
Vax: tn zadał dobre pytanie, dużo osób korzysta ze wzoru sin(α+β) = sinαcosβ+sinβcosα nie wiedząc, skąd on się bierze, przedstawię pewien dowód, korzystając z rysunku wyżej mamy:

	h
{cosα =
	a

	h
{cosβ =
	b

⇔ {h = acosα {h = bcosβ Zauważmy teraz, że pole trójkąta można policzyć na dwa sposoby, raz dodając P₁ + P₂ oraz P =

	absin(α+β)		ahsinα		bhsinβ
		, oczywiście P1 =		, P2 =		porównajmy obie strony:
	2		2		2

absin(α+β)		ahsinα+bhsinβ
	=		/*2
2		2

absin(α+β) = ahsinα+bhsinβ Teraz po prawej stronie pod pierwsze ,,h" podstawiamy bcosβ, a w drugiem acosα: absin(α+β) = absinαcosβ + absinβcosα /:ab sin(α+β) = sinαcosβ+sinβcosα cnd Pozdrawiam.

tn: Vax wielkie dzięki za wyjaśnienie, jak będzie coś niejasne to będę pisał

tn: Vax wielkie dzięki za wyjaśnienie, jak będzie coś niejasne to będę pisał

tn: Vax wielkie dzięki za wyjaśnienie, jak będzie coś niejasne to będę pisał

Jack: Jakiś komentarz by się przydał, dlaczego wzór działa nie tylko dla kątów ostrych w trójkącie.