pole figury bjornolf: Oblicz pole figury ograniczonej funkcjami f i g: f(x)=−x²+2x+3 g(x)=x+1 f(x)będzie ''na górze", więc: Pf=∫ (f(x)−g(x)) dx

	x3		x2
Pf=∫ −x2+x+2 dx = −∫x2dx + ∫xdx +∫ 2dx = −		+		+ 2x
	3		2

obliczanie punktów wspólnych i wyszło, że √Δ=√17?

Marcin: wydaje mi się, że to trzeba całką podwójną liczyć ∫∫1dxdy po obszarze D, który jest ograniczony tymi funkcjami, co napisałeś Najlepiej narysuj sobie wykresy tych funkcji szkicowo, zobacz jak się zmieniają x i y i to Ci da granice całkowania, a potem to już z górki

bjornolf: mhm, bo myślałem, że można zastosować wzór na pole figury ograniczonymi krzywymi funkcji. wtedy jak znajdę miejsca wspólne to bedzie to równoznaczne, ze będę miał całkę oznaczoną do obliczenia. Ograniczoną tymi punktami wspólnymi. no a dalej to podstawiam odpowiednio do wzoru za x te ograniczenia i dodaje do siebie otrzymując teoretycznie prostą liczbę.

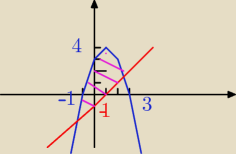
bjornolf: tak?

Marcin: ten czerwony wykres chyba o dwie jednostki w górę powinien pójść

bjornolf: o ja, a zapisałem sobie na kartce g(x)=x−1...

Marcin: wtedy obszar D: −1≤x≤2 x+1≤y≤−x²+2x+3 i piszesz całkę dx całkujesz w granicach od −1 do 2, a po dy w granicach tak jak równania

bjornolf: czyli już widać, że punktem wspólnym będzie {−1,x} teraz mogę tak obliczyć tą drugą współrzędną?: y=−x²+2x+3 no a poza tym, wyjdzie, że Δ=9 wiec x₁=2, a x₂ = −1 czyli sie zgadza ciekawi mnie jednak sposób całką podwójną(może dlatego, że obowiązuje jej znajomość, a ćwiczeniowcy nie wystarczyło czasu na wytłumaczenie jakbyś miał czas mógłbyś rozwiązać to twoim sposobem? jak będę sobie przyswajał ten dział, to powrócę do tego przykładu. oczywiście nic na siłę

kibix: ∫dx∫dy w pierwszej calce granice od −1 do 2 w drugiej x+1 do −x2+2x+3 Musi to samo wyjsc całka z dy to po prostu y i podstawiasz granice (−x2+2x+3 −(x+1)) i liczysz z tego 2 calke od −1 do 2

bjornolf: mhm, czyli zwyczajnie pod ∫ wpisuje x+1, a na górze∫ −x2+2x+3. ok, potrenuje jeszcze to, później, dziękuję serdecznie Wam za pomoc

Magda: bjornoff jak tam macierze : DD hah ; ) przydały się troche moje tłumaczenia

bjornolf: no pewnie, zaliczenie otrzymane, więc mogę iść na egzamin nr 1 co do pytań: Agh−metalurgia;wydział odlewnictwa

Magda: no ja czekam aktualnie a wyniki poprawy jednego kolokiwum z matmy bo czeka mnie egzamin z teori z matmy jeszcze macierze to ja miałam w październiku xD ja UMK Toruń− Finanse i rachunkowość 1r.

Marcin: chyba kibix już wszystko napisał(a) więc nie mam nic do dodania wydaje mi się, ze całką podwójną jest trochę przejrzyściej to liczyć, ale to widać kwestia indywidualna... ja jutro mam egzamin z matmy z całek ale chyba nie idę w sumie 3,5 z zerówki już jest, ale ciągle się zastanawiam czy nie pójść spróbować poprawić

bjornolf: mój znajomy, także na finansach, także zaczynał matematykę od macierzy

bjornolf: jak bez konsekwencji, to na Twoim miejscu poszedłbym

Magda: bo macierze np na TI nam się powtarzają w excelu

Marcin: bjornolf−jak napiszę gorzej (3 lub 2) to wpisuje tą gorszą ocenę...egzamin za 45 minut a jeszcze nie podjąłem decyzji ja na Politechnice zaczynałem od zespolonych, a później były macierze