okrąg opisany na czworokącie kk: W trapezie równoramiennym długosci podstaw są równe 5 i 3. Oblicz długosc promienia okręgu opisanego na tym trapezie, jeśli jego kat ostry ma miarę 60 stopni

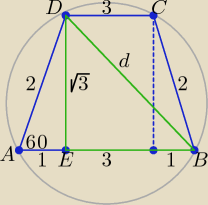
Bogdan: Korzystamy z własności trójkąta prostokątnego o kącie ostrym 60^o. Na tej podstawie otrzymujemy długość ramienia = 2 oraz długość wysokości = √3. d = √3 + 16 = √19 Okrąg opisany na trapezie jest jednocześnie okręgiem opisanym na trójkącie ABD. Długość promienia okręgu opisanego można wyznaczyć z twierdzenia sinusów w trójkącie ABD:

	d		|AB|*|BD|*|AD|
R =		albo z zależności: R=		, gdzie: PΔ to pole trójkąta.
	2sin60o		4*PΔ

ICSP: Bogdan a nie łatwiej z twierdzenia cosinusów to policzyć? Bo przynajmniej u mnie na lekcjach nie było tego ostatniego wzorku

Bogdan: ale co chcesz obliczyć z twierdzenia cosinusów?

Bogdan: To, że czegoś nie było na lekcjach nie usprawiedliwia nieznajomości zagadnienia. Pole trójkąta o bokach długości a, b, c oraz długości promienia okręgu opisanego R

	a*b*c		a*b*c
wyraża się wzorem: P =		, stąd R =		.
	4R		4*P

ZKS: O to chodziło ICSP Bogdanie d² = 29 − 10 d = √19

ICSP: Chodziło mi o to że jeżeli z wierzchołków D i B poprowadzimy promienie to utworzy się Trójkąt równoramienny z tych dwóch promieni oraz odcinka BD. Kąt w tym trójkącie będzie wynosił 120^o i znajdował się miedzy promieniami.

Bogdan: Ciekawy ICSP pomysł, ale dochodzi tu dodatkowy krok polegający na zastosowaniu twierdzenia o kącie wpisanym i środkowym opartych na tym samym łuku. Wzór sinusów daje od razu odpowiedź i jest prostszy rachunkowo od wzoru cosinusów.