stereometria
tomq: Dany jest ostrosłup prawidłowy czworokątny. Krawędź podstawy ostrosłupa ma długość3. Kąt
dwuściennny między sąsiednimi ścianami ma 120 stopni. Oblicz długość krawędzi bocznej tego
ostrosłupa. Proszę o pomoc

15 cze 18:24
tomq: ?
15 cze 19:31
kris:
15 cze 19:38
TOmek:
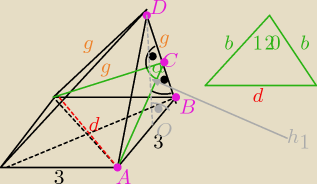
α=120
d=a
√2=3
√2
(3
√2)
2=b
2+b
2−2(3
√2)*b*cos120
h
1=
1,5
2+(h
1)
2=g
2,
h
12=g
2−2,25
h
1=
√g2−2,25
AC jest wys. trójkąta ABD, odcinek DO jest wys. trójkąta ABD, porównuje pola
wyznaczamy "g" i mamy wynik

15 cze 20:20
TOmek: chyba cos spieprzyłem ...
15 cze 20:25
ha ha:
nawet rysunek spieprzyłeś, co to jest na tym rysunku?, bo na pewno nie jest ostrosłup
prawidłowy
15 cze 21:07
TOmek:
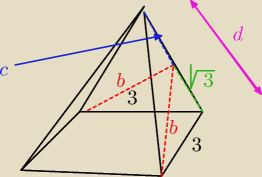
tak własnie na tamtym rysnuku jest ostroslup prawidłowy!
b=
√6 źle obliczyłem wczesniej
więc: BC=
√3
2,25+h
2=3
d=
15 cze 22:12
Bogdan:
TOmek − żaden Twój rysunek nie przedstawia ostrosłupa prawidłowego czworokątnego
i mówiąc szczerze, to są jakieś koszmarne bazgroły, a nie staranny rysunek.
16 cze 00:05
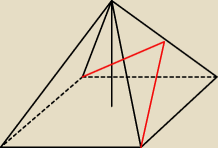
ICSP:
16 cze 00:20
Bogdan:
Rysunek ICSP jest poprawny i jeśli spodek wysokości ostrosłupa leży w punkcie przecięcia
przekątnych kwadratowej podstawy, to przedstawia ostrosłup prawidłowy czworokątny.
Czy tak tu jest?
16 cze 00:41

 α=120
d=a√2=3√2
(3√2)2=b2+b2−2(3√2)*b*cos120
α=120
d=a√2=3√2
(3√2)2=b2+b2−2(3√2)*b*cos120

 tak własnie na tamtym rysnuku jest ostroslup prawidłowy!
b=√6 źle obliczyłem wczesniej
więc: BC=√3
2,25+h2=3
tak własnie na tamtym rysnuku jest ostroslup prawidłowy!
b=√6 źle obliczyłem wczesniej
więc: BC=√3
2,25+h2=3
