2 przykłady z logarytmów, których nie ogarniam Xiaton: 1) rozwiąż równanie log₂(log₄x)=1 2) rozwiąż nierówność 2log_¹3x < log_¹3(5x−6)

Xiaton: pomógłby mi ktoś

Ajtek: W czym problem?

krystek: def log w pierwszym przykładzie 2¹=log₄x i jeszcze raz z def imasz zadanie . Pamiętaj o zał 1)x>0 i log₄x>o @)2logx=logx² i pamiętaj ,że podstawa log jest ułamkiem więc zmieniamy znak nierówności.

Ajtek:

	4
Nie tyle ułamkiem co mniejsza od 1. Gdy		jest w podstawie (też jest ułamkiem), a znaku
	3

nie zmieniamy przecież.

Xiaton: nie mam głowy do logarytmów, 1 w miarę rozumiem, ale nie wiem skąd w 2 ci się to wzięło

Ajtek: Z def.: log_ab=c w.t.w gdy a^c=b log₂(log₄x)=1 2¹=(log₄x)

Xiaton: dzięki ale to akurat rozkminiam, chodzi mi o 2 przykład

krystek: Jak dokładnie to :0 < a<1

Ajtek: Tak wiem, tylko mi jeden klawisz nie działa, ten kluczowy w tym przedziale .

Ajtek: Jedna z własności logarytmów: log_ab^c=clog_ab

krystek: x²>5x−6 przy zał.x>0 i 5x−6>0

Xiaton: skąd wzięło ci się x²

Xiaton: aha już wiem

Xiaton: dzięki za pomoc

Xiaton: no a jak mam x² > 5x−6 to co dalej, bo przecież funkcją kwadratową nierówności nie obliczę

Xiaton: wie ktoś

Ajtek: Jak to nie

Ajtek: Licz pierwiastki

Xiaton: przecież w f. kwadratowej jest: ax² + bx² + c = 0 a tutaj jest nierówność

Ajtek: Licz pierwiastki, napisz co wyszło, różnica polega na tym, iż w równaniu masz dwa rozwiązania, a w nierówności masz przedział/y.

Xiaton: jakie pierwiastki

Ajtek: A jakbyś rozwiązał takie równanie: x²=5x−6

Xiaton: aha, czyli będzie x₁ i x₂ , dobra dzięki dalej sobie poradzę

Ajtek: No, napisz finalny wynik, zobaczymy czy dobry.

Xiaton: x₁=2 x₂=3

Ajtek: Jest ok, tylko mamy nierówność, odpowiedzią będą więc przedziały. Podaj je.

Xiaton: ...

Xiaton: czyli co

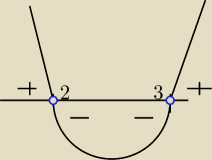
Ajtek: No właśnie. Jeżeli mamy równanie to mamy dwa rozwiązania w tym przypadku, takie jak podałeś. W przypadku nierówności są przedziały. Zauważ, że np. dla x=0 ta nierówność również jest prawdziwa. Dla x=4 też jest prawdziwa. Na rys. powyżej widać kiedy jest dodatnia a kiedy ujemna. x€(−∞;2)u(3;∞). 2 i 3 nie spełniają tej nierówności, ponieważ dla tych argumentów wartość jest równa 0.

Xiaton: aha czyli parabola, wytłumacz mi jeszcze tylko, dlaczego nie jest odwrotnie, czyli między 2, a 3 dodatnie, a reszta ujemne

Ajtek: Ramiona paraboli skierowane do góry, ponieważ a>0. Gdybyśmy mieli np. −x² wówczas ramiona w dół bo a mniejsze 0 i wtedt byłby przedział (2;3).

Xiaton: i wszystko jasne, wielkie dzięki sam bym tego nie ogarnął, a mam to na jutro

Ajtek: Ogarnąłbyś, ogarnął. Tylko f. kwadratową trzeba stosować.