PROblem TOmek: Znajdź najmniejszą i najwiekszą wartość funkcji f(x)=−cos²x−4cosx+5

oaxoaxoax: Nie robiłem tego, ale pomysł . cos x=t f(x)−t²−4t+5 ⇒ Mamy równanie kwadratowe, a więc należy szukać p oraz q . Tak mi się zdaje, chociaż tak jak napisałem na początku, nie robiłem tego jeszcze nigdy .

TOmek: na bank nie ,bo cos tam ma być ,ze t musi nalezec do <−1,1> , czekam na eskperta

oax: He, cóż pudło . Tak więc, czekajmy na kogoś mądrzejszego .

ZKS: Jak podstawiamy zmienna t to funkcja powinna być h(t) , g(t). t = sinx t∊<−1,1> h(t) = −t² − 4t + 5 t_w = −2 nie należy do przedziału <−1,1> h(−1) = 8 h_max = 8 dla x = −1 h(1) = 0 h{min} = 0 dla x = 1

TOmek: pasuje z odp. dziekuje

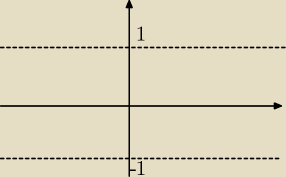
TOmek: nie rozumiem czegoś przecierz powinniśmy szukać(dla jakiegos argumenty y=−1) −1=h(t), przecież szukamy wartosci które sie mieszczą w "y" od <−1,1>

ZKS: Na zdrowie

ZKS: Jeżeli podstawimy t = sin x to mamy zwykłą funkcję kwadratową. Musimy zbadać jakie ona przyjmuje wartości na przedziale <−1,1> i (bo takie wartości przyjmuje t = sin x)

ZKS: Jeżeli podstawimy t = sin x to mamy zwykłą funkcję kwadratową. Musimy zbadać jakie ona przyjmuje wartości na przedziale <−1,1> i (bo takie wartości przyjmuje t = sin x)

siemka: t = (cosx)−2c t' = (cosx)' = −sinx f'(x) = (−cos²x)' = (−t²)' = −2t * t' = −2cosx * −sinx = 2sinxcosx (−4cosx)' = −4(cosx)' = −4 * −sinx = 4sinx (5)' = 0 czyli f'(x) = 2sinxcosx + 4sinx = 0 ale co dalej ^^

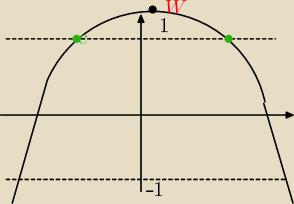
TOmek: t<0 ramiona ku dołowi pierw patrze czy wierzchołek funkcji zawiera sie w <−1,1>

	−Δ		−36
Wy=		=		=9 nie nalezy do <−1,1>
	4a		−4a

czyli najwiekszą wartość funkcji h(t) dla sinusa znajduje sie dla y=1 (zielony punkt) czyli powinniśmy poszukać 1=−t²−4t+5 co jest błędnego w moim rozumowaniu (dodam ,ze 5h juz siedze nad trygonometrią, wiec moge czegos głupiego nie widziec)

TOmek: bez całek i pochodnych prosze

TOmek: Godziom, pomozesz?

TOmek: *Godzio

rumpek: y = −t² − 4t + 5 Δ = 16 + 20 = 36

	4
xw =		= −2
	−2

	−36
yw =		= 9
	−4

Patrzysz na x_w nie należy do przedziału <−1,1>, więc: f(1) = −1 − 4 + 5 = 0 <−min f(−1) = −1 + 4 + 5 = 8 <− max https://matematykaszkolna.pl/strona/87.html :(

Bogdan: f(x) = −cos²x − 4cosx + 5 i cosx∊<−1, 1>. cosx = t i t∊<−1, 1>. Zadanie sprowadza się do wyznaczenia najmniejszej i największej wartości funkcji f(t) = −t² − 4t + 5 dla t∊<−1, 1>. Najpierw sprawdzamy, czy odcięta wierzchołka paraboli należy do przedziału <−1, 1>.

	4
tw =		= −2∉<−1, 1>.
	−2

Nie wyznaczamy więc f(−2), natomiast wyznaczamy: f(−1) = −1 + 4 + 5 = 8, f(1) = −1 − 4 + 5 = 0 Odp.: f_max = 8, f_min = 0

TOmek: rozumiem, kurna musiałem miec mocne zacmienie by tego nie zrozumiec, wystarczy sobie to narysowac, dziekuje Panowie