 W trójkącie ABC dane są AB=10 ABC=60◯ , kąt ACB= 45◯ . Oblicz długości pozostałych boków tego
trójkąta, jego pole oraz promień okręgu opisanego na tym trójkącie.
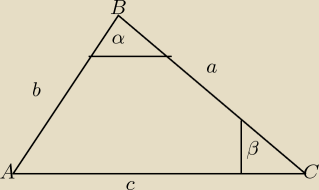
Zrobiłem sobie tak rysunek,
α=60◯
β=45◯
|AB|=10
czy aby wyliczyć długości boków powinienem utworzyć układ równań
b2=a2+c2−2ac cos 45◯
c2=a2+b2−2ab cos60◯
W trójkącie ABC dane są AB=10 ABC=60◯ , kąt ACB= 45◯ . Oblicz długości pozostałych boków tego
trójkąta, jego pole oraz promień okręgu opisanego na tym trójkącie.
Zrobiłem sobie tak rysunek,
α=60◯
β=45◯
|AB|=10
czy aby wyliczyć długości boków powinienem utworzyć układ równań
b2=a2+c2−2ac cos 45◯
c2=a2+b2−2ab cos60◯
| b | c | |||
i czy aby wyliczyć R mam skorzystać z | = | =2R  | ||
| sinβ | sinα |
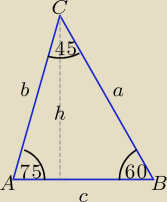 c = 10
c = 10
| 10 | a | b | ||||
z twierdzenia sinusów: | = | = | = 2R | |||
| sin45o | sin75o | sin60o |
| 1 | 1 | 1 | ||||
pole P = | absin45o = | acsin60o = | bcsin75o | |||
| 2 | 2 | 2 |