Oblicz wartość pozostałych funkcji trygonometrycznych mając dane: Mariusz N.: a) sinu={5}{13} , b) tg=3

metcub: Łatwe ale sporo pisania: a) sin² α + cos² α = 1 (⁵₁₃)² + cos² α = 1 ²⁵₁₆₉ + cos² α = 1 cos² α = 1 − ²⁵₁₆₉ cos² α = ¹⁴⁴₁₆₉ cos α = ¹²₁₃ (zakładam że kąt jest ostry, w przeciwnym wypadku dochodzi jeszcze cos α = − ¹²₁₃) tg α = ^sinα_cosα = ⁵₁₃ : ¹²₁₃ = ⁵₁₃ * ¹³₁₂ = ⁵₁₂ ctg α = ¹²₅ (jako że jest to odwrotność tg)

ZKS: Łatwiejsze gdy wie się że 5,12,13 to trójka pitagorejska.

	5
Skoro sinx =		to wiemy że:
	13

	12		12
cosx =		lub cosx = −
	13		13

	5		5
tgx =		lub tgx = −
	12		12

	12		12
ctgx =		lub ctgx = −
	5		5

ZKS: tgx = 3

	1
cosx =
	√1 + tg2x

	√10		√10
cosx =		lub cosx = −
	10		10

	3√10		3√10
sinx =		lub sinx = −
	10		10

	1
ctgx =
	3

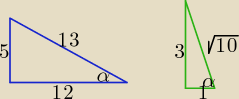
Bogdan: Proponuję tak: Z twierdzenia Pitagorasa wyznaczamy długość trzeciego boku i piszemy odpowiedź:

	5
sinα =		,
	13

	12		−12
cosα =		lub cosα =		bo brak informacji o tym, że kąt jest ostry,
	13		13

	5		−5
tgα =		lub tgα =
	12		12

	12		−12
ctgα =		lub ctgα =
	5		13

Podobnie postępujemy w drugim przypadku.