Punkty A=(-2,3) i B=(5,4) są wierzchołkami trójkąta prostokątnego ABC o przeciwp Michal: Punkty A=(−2,3) i B=(5,4) są wierzchołkami trójkąta prostokątnego ABC o przeciwprostokątnej AB. Wierzchołek C leży na osi OX. Oblicz współrzędne punktu C

Bogdan: C = (x, 0) (−2 − x)² + (3 − 0)² = (5 − x)² + (4 − 0)²

Gustlik: Bogdan, a skąd wiesz, że |AC|=|BC|? Nic nie pisze w zadaniu, żeby był to trójkąt równoramienny. Ja bym to rozwiazał iloczynem skalarnym wektorów. Wiadomo, że kąt C jest prosty, czyli wektor CA^→ jest prostopadły do CB^→. Liczę współrzędne wektorów CA^→ i CB^→: CA^→=[−2−x, 3−0]=[−2−x, 3] CB^→=[5−x, 4−0]=[5−x, 4] Korzystam ze wzoru na iloczyn skalarny: u^→*v*→=u_xv_x+u_yv_y CA^→*CB^→=(−2−x)(5−x)+3*4=−10+2x−5x+x²+12=x²−3x+2 Warunek prostopadłosci wektorów: iloczyn skalarny = 0. x²−3x+2=0 Δ=9−4*1*2=9−8=1 √Δ=1

	3−1
x1=		=1
	2

	3+1
x2=		=2
	2

Zatem są dwa rozwiązania: C₁=(1, 0), lub C₂=(2, 0).

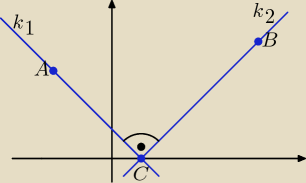
Bogdan: Tak, masz rację Gustliku, brak w zadaniu informacji o tym, że |AC| = |BC|. Proponuję więc takie rozwiązanie: C = (x, 0),

	−3
prosta zawierająca punkty A i C k1: y = a1x + b1, a1 =		,
	x + 2

	−4
prosta zawierająca punkty B i C k2: y = aax + ba, a2 =		,
	x − 5

	−3		−4
k1⊥k2 ⇒ a1 * a2 = −1 ⇒		*		= −1 ⇒ x2 − 3x + 2 = 0
	x + 2		x − 5

Stąd x = 1 lub x = 2

Gustlik: Też dobry i szybki sposób. Niemniej ja dużo staram się rozwiazywac zadań z geometrii analitycznej wektorami, bo jakiś za przeproszeniem debil z MEN wycofał je z podstaw, a rachunek wektorowy jest bardzo prosty i znacznie przyspiesza rozwiązywanie tego typu zadań, dlatego ja pokazuję te metody, abu uczniowie się z nimi zapoznali, bo na maturze liczy się poprawność rozwiązania, a wybór metody to sprawa ucznia, można nawet użyć całek i pochodnych funkcji, jeżeli uczeń je zna, ważne jest tylko, żeby nie było błędu. Dlatego pokazuję metody proste i szybkie nie bacząc na to, czy są w programie podstawowym czy rozszerzonym, zwlaszcza że na podstawach wiele zadań robi się dłuższymi metodami, niż na rozszerzeniu. Pozdrawiam.