wielomiany
Paula: 1. Liczby 3 i -1 są pierwiastkami wielomianu W(x)=2x3+ax2+bx+30
a) Wyznacz wartości współczynników a i b.
b) Oblicz trzeci pierwiastek tego wielomianu.
2. Dane są wielomiany: Q (x)=x4-8x3+22x2-24x+9 oraz P(x)=2x3-9x2+7x+6. Oblicz
wartości m i n, dla których wielomian W(x)=x4+(m-4)x3-(2n+6)x2-38x-3 równy jest
wielomianowi Q(x)-2P(x)
3. Wielomian W(x)=-2x4+5x3+9X2-15X-9 jest podzielny przez dwumian (2x+1). Wyznacz
pierwiastki tego wielomianu.
3 mar 09:31
Paula: Czy mozecie mi pomóc

3 mar 10:36
Paula: Bardzo prosze o pomoc, ja naprawde tego nie rozumiem. Czy możecie pomóc


4 mar 10:05
Szymon: skoro nie ma chętnych do pomocy to ja się skuszę

zadanie 1
a)
W(3)=54+9a+3b+30=0
W(-1)=-2+a-b+30=0
z tego robimy układ równań:
9a+3b+84=0 /:3
a-b+28=0
3a+b+28=0
a-b+28=0 +
----------------------
4a=-56
a=-14
b=14
wielomian ma postać W(x)=2x
3 -14x
2 +14x +30
po skróceniu przez 2 mamy W(x)= x
3 -7x
2 +7x +15
b)
najszybciej będzie zastosować Hornera: (wiemy że 3 pierwiastkiem wielomianu)
1 -7 7 15
3 1 -4 -5 0
W(x)= (x-3)( x
2 - 4x -5)
x
2 - 4x - 5
Δ= 16+20=36
√Δ = 6
x
1 = (4-6)/2= -1
x
2 = (4+6)/2= 5
Po rozkładzie wielomian ma postać W(x)= (x-3)(x+1)(X-5)
trzecim pierwiastkiem jest liczba 5
4 mar 11:16
Szymon: zadanie 2
najpierw musimy policzyć ile to jest Q(x) - 2P(x)
Q(x)= x4-8x3+22x2-24x+9
P(x)= 2x3-9x2+7x+6
2P(x)= 4x3 - 18x2 +14x +12
Q(x) - 2P(x)= x4 - 8x3 +22x2 - 24x +9 - 4x3 +18x2 - 14x -12 = x4 -12x3 +40x2 -38x
-3
W(x)=x4+(m-4)x3-(2n+6)x2-38x-3
wielomiany są sobie równe kiedy ich współczynniki są równe czyli:
(m-4) = -12
m=-16
-2n - 6 = 40
2n=-46
n = -18
Odp. m= -16 , n= -18
4 mar 11:24
Bogdan:
Uwaga do Szymona.
Wielomian W(x) po podzieleniu przez 2 jest równy (1/2)*W(x), nie jest jednak dalej
wielomianem W(x).
Wielomiany:
W(x) = 2x3 -14x2 + 14x + 30
V(x) = x3 - 7x2 + 7x + 15
nie są równe.
4 mar 11:30
Szymon: zadanie 3.
to jest typowe zadanie na dzielenie wielomianu, zajrzyj sobie do podręcznika i zobacz jak
się dzieli wielomian przez dwumian. można to rozwiązać innym sposobem ale mi się już
niestety nie chce tego tu wklepywać. z pewnością sama dasz sobie z tym rade.
4 mar 11:31
Paula: Bogdan czyli coś jest źle w rozwiązniu Szymona

pomóż bo ja sie wogóle nie orientuje w
tych wielomianach. z góry dzięki
4 mar 12:07
Bogdan:
ad 1.
Można wyznaczyć wartości współczynników a, b oraz warość trzeciego pierwiastka x3
w jednym kroku.
Zapisujemy wielomian W(x) w postaci iloczynowej:
W(x) = 2(x - 3)(x + 1)(x - x3)
Wykonujemy mnożenie i porządkujemy wynik wg potęg zmiennej x:
W(x) = 2x3 + (-4 - 2x3)x2 + (-6 + 4x3) + 6x3
Porównujemy współczynniki przy jednakowych potęgach x:
przy x3: 2 = 2
przy x2: a = -4 - 2x3
przy x1: b = -6 + 4x3
przy x0: 30 = 6x3 stąd x3 = 5 oraz a = -4 - 2*5 = -14, b = -6 + 4*5 = 14
Odp.: W(x) = 2x3 - 14x2 + 14x + 30, trzeci pierwiastek x3 = 5
4 mar 12:08
Paula: Bogdan serdeczne dzieki za 1 zadanie, ale czy mógłbyś jeszcze spojrzec na 2 i 3.

ja nie
wiem jak sie do tego zabrac a muszę to już na jutro mieć

4 mar 12:13
Szymon: Dobrze Bogdan, że zauważyłeś.
Paula, zadania jest rozwiązane poprawnie po prostu wielomian W(x) skrócony przez 2 nie
może nadal być wielomianem W(x) ale może być np. V(x) tak jak napisał Bogdan. To jest
kwestia nazwy, jednakże jest to istotne aby zadanie było poprawnie rozwiązane, także
przepisz sobie V(x) a nie W(x).
Oczywiście wyniki są poprawne.
4 mar 12:13
Bogdan:
Paulo: W rozwiązaniu Szymona jest wszystko dobrze za wyjątkiem ostatecznej postaci
wielomianu W(x).
Wielomian W(x) wyraża się wzorem W(x) = 2x3 - 14x2 + 14x + 30.
Taką postać podał również Szymon, ale potem błędnie podał inną postać tego
wielomianu stwierdzając, że W(x)= x3 -7x2 +7x +15, co nie jest prawdą.
Poprawnie byłoby ewentualnie: W(x)= 2(x3 -7x2 +7x +15), czyli wyłączając 2
przed nawias, a nie dzieląc W(x) przez 2, bo dzielenie wielomianu daje w wyniku
nowy i inny wielomian
4 mar 12:15
Paula: Wielkie dzieki za wytłaumaczenie, już troche rozumiem, mam jeszcze pytanko czy odpowiedź
b do 1 zadania napisana przez Szymona jest poprawna

4 mar 12:21
Bogdan:
ad 2.
Q(x)-2P(x) = x4 - 12x3 + 40x2 - 38x - 3 (tak, jak podał Szymon)
W(x)=x4 + (m - 4)x3 + (-2n - 6)x2 - 38x - 3
Porównujemy współczynniki przy tych samych potęgach:
przy x3: m - 4 = -12 stąd m = -8
przy x2: -2n - 6 = 40 stąd n = -23
Odp.: m = -8, n = -23
4 mar 12:28
Bogdan:
Paulo, podaj swoje rozwiązanie zadania 3, sprawdzę.
Podziel, tak jak sugerował Ci Szymon, wielomian W(x) przez (2x + 1), potem
rozłóż otrzymany w wyniku dzielenia wielomian na czynniki metodą grupowania
i wyłączania przed nawias.
4 mar 12:39
Paula: Wynik wyszedł mi -x
3+3x
2+3x-9 dobrze

ale i tak nie weim jak dalej pogrupowac i
wyłączyć przed nawias
4 mar 12:59
Bogdan:
Dobrze.
-x3 + 3x2 + 3x - 9 = -x2(x - 3) + 3(x - 3) =
czy potrafisz dalej poprowadzić rozwiązanie?
4 mar 13:05
Paula: czy to będzie (x-3)(-x
2+3) pierwiastki x=3 i x=√3≈1,71

4 mar 13:11
Paula: Bogdan czy dobrze

4 mar 13:18
Bogdan:
Nie do końca dobrze.
Powinno być tak:
-x2(x - 3) + 3(x - 3) = -(x - 3)(x2 - 3) = -(x - 3)(x - √3)(x + √3)
x1 = 3, x2 = √3, x3 = -√3.
Nie podaje sie przybliżonych wartości, jeśli nie ma takiego wyraźnego
polecenia w zadaniu.
4 mar 13:27
Paula: 
4 mar 13:28
Paula: Wielkie dzięki Bogdan za pomoc
4 mar 13:29
Bogdan:
W(x) = -(x - 3)(x - √3)(x + √3)(2x + 1)
Ostateczna postać wielomianu:
W(x) = -2(x - 3)(x - √3)(x + √3)(x + 1/2)
Jest więc jeszcze x4 = - 1/2
4 mar 13:30
Justysia: Justysia: Witajcie!
Pomóżcie mi proszę bo mam pracę od której wszystko zależy a nic nie czaję a zadania są z
wielomianów:
1. Rozłóż wielomiany na czynniki:
a. −5x4+3x3+14x2
b. x3+x2−3x−6
c. −2x3+x2+18x−9
d. x5−6x4−40x3
2. Rozwiąż równania:
a. x3−2x2+2x−4=0
b. −4x3−4x2+3x=0
3. Znajdz współczynniki m i n wielomianu W(x)=x3+mx2+nx+12 wiedząc, że jego pierwiastkami są
liczby −3 i 4.
Jeśli ktoś mi to rozwiąże będę na serio wdzięczna...
16 wrz 08:37
TOmek : a) wyciągnij x2 przed nawias i masz równanie kwadratowe
b)chyba źle przepisałas, bo jak dobrze to musisz z tw. o pier. wym. sprawdzić czy ma
pierwiastek
c) −x2(2x−1)+9(2x−1)=(−x2+9)(2x−1)=(2x−1)(3−x)(3+x)
d)x3 wyciągi przed nawias i masz równanie kwadratowe.
16 wrz 09:39
TOmek : 2.a) x2(x−2)+2(x−2)=(x−2)(x2+2)
pamiętaj ,ze x2 +2 nie ma pierw.
b)wyciągnij x przed nawias i równanie kwadratowe.
3. podstawiasz pierw to tego wielomianu
(−3)3+m(−3)2+n(−3)+12=0
43+m42+n4+12=0
układ równań
16 wrz 09:43
TOmek : b)wyciągnij x przed nawias i masz równanie kwadratowe
16 wrz 09:44
TOmek :
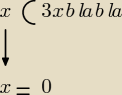
16 wrz 09:50
mm: W(x)3x3−3x+1V(x)2x2−4
9 mar 19:13
Paucia: Wyznacz współczynniki a i b dla których wielomiany
P(x)= (x2 − 2)2 i Q(x)= x4 + (a+5) +bx2 +4 są równe.
6 cze 19:47
Paucia: Dane są wielomiany W(x)= −8+4 , P(x)= 5x2 + 2x + 4 oraz Q(x)= x2−x+4.
Wyznacz wielomian 1/4W(x)(P(x)−Q(x))
6 cze 19:51
klaudia: 8x3−1
23 wrz 22:58
Kostek:
(2x−1)(4x2+2x+1)
23 wrz 23:00
klaudia: ale mozesz to rozpisac jak to liczyles?
23 wrz 23:25
5-latek: Wzor skroconego mnozenia a3−b3= zobacz sobie
gdzie a=2x bo (2x)3=8x3 i b=1 bo 13=1 i teraz rozpisz sobie sama
23 wrz 23:29
klaudia: dzieki
23 wrz 23:32
Fajna 20: Dany jest wielomian W(x)=2x3+(a+2)x2−3x+b wiadomo że W(1)=8 i W(−2)=14
wyznacz pierwiastki wielomianu G(x)=W(x)−2x3+15
30 gru 17:07
Fajna 20: Prosze o pomoc
30 gru 17:10
Fajna 20: Prosze o pomoc
30 gru 17:10
5-latek: Naprawde jestes fajna i masz 20 lat?
To w takim razie
Ja mam 20 lat , Ty masz 20 lat ,przed nami siodme niebo 
a odpowiesz na pytanie to pomoge dalej

30 gru 17:15
5-latek: No i jak
fajna 20 
30 gru 17:23
Fajna 20: A nie możesz poprostu mi pomóc ?
2 sty 14:13
5-latek: Ale nie odpowiedzialas na moje pytanie czy jestes fajna i masz 20 lat ?

2 sty 14:26
olo: to chyba chodzi o to, że ona myśli, że jest fajna już 20 raz

2 sty 14:34
Fajna 20: Tak. Pomożesz mi z tym zadaniem czy nie?
2 sty 14:37
5-latek: NO to skoro jestes fajna

to najpierw wyznaczymy postac wielomianu W(x)
2*(1)
3+(a+2)*1
2−3*(1)
3+b=8
2*(−2)
3+(a+2)*(−2)
2−3*(−2)+b=14 wyznacz z tego wspolczynniki a i b i napisz jak jest
postac wielomianu W(x)
2 sty 14:43
Fajna 20: 

2 sty 19:41



 zadanie 1
a)
W(3)=54+9a+3b+30=0
W(-1)=-2+a-b+30=0
z tego robimy układ równań:
9a+3b+84=0 /:3
a-b+28=0
3a+b+28=0
a-b+28=0 +
----------------------
4a=-56
a=-14
b=14
wielomian ma postać W(x)=2x3 -14x2 +14x +30
po skróceniu przez 2 mamy W(x)= x3 -7x2 +7x +15
b)
najszybciej będzie zastosować Hornera: (wiemy że 3 pierwiastkiem wielomianu)
1 -7 7 15
3 1 -4 -5 0
W(x)= (x-3)( x2 - 4x -5)
x2 - 4x - 5
Δ= 16+20=36
√Δ = 6
x1 = (4-6)/2= -1
x2 = (4+6)/2= 5
Po rozkładzie wielomian ma postać W(x)= (x-3)(x+1)(X-5)
trzecim pierwiastkiem jest liczba 5
zadanie 1
a)
W(3)=54+9a+3b+30=0
W(-1)=-2+a-b+30=0
z tego robimy układ równań:
9a+3b+84=0 /:3
a-b+28=0
3a+b+28=0
a-b+28=0 +
----------------------
4a=-56
a=-14
b=14
wielomian ma postać W(x)=2x3 -14x2 +14x +30
po skróceniu przez 2 mamy W(x)= x3 -7x2 +7x +15
b)
najszybciej będzie zastosować Hornera: (wiemy że 3 pierwiastkiem wielomianu)
1 -7 7 15
3 1 -4 -5 0
W(x)= (x-3)( x2 - 4x -5)
x2 - 4x - 5
Δ= 16+20=36
√Δ = 6
x1 = (4-6)/2= -1
x2 = (4+6)/2= 5
Po rozkładzie wielomian ma postać W(x)= (x-3)(x+1)(X-5)
trzecim pierwiastkiem jest liczba 5
 pomóż bo ja sie wogóle nie orientuje w
tych wielomianach. z góry dzięki
pomóż bo ja sie wogóle nie orientuje w
tych wielomianach. z góry dzięki
 ja nie
wiem jak sie do tego zabrac a muszę to już na jutro mieć
ja nie
wiem jak sie do tego zabrac a muszę to już na jutro mieć

 ale i tak nie weim jak dalej pogrupowac i
wyłączyć przed nawias
ale i tak nie weim jak dalej pogrupowac i
wyłączyć przed nawias



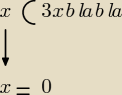
 a odpowiesz na pytanie to pomoge dalej
a odpowiesz na pytanie to pomoge dalej 



 to najpierw wyznaczymy postac wielomianu W(x)
2*(1)3+(a+2)*12−3*(1)3+b=8
2*(−2)3+(a+2)*(−2)2−3*(−2)+b=14 wyznacz z tego wspolczynniki a i b i napisz jak jest
postac wielomianu W(x)
to najpierw wyznaczymy postac wielomianu W(x)
2*(1)3+(a+2)*12−3*(1)3+b=8
2*(−2)3+(a+2)*(−2)2−3*(−2)+b=14 wyznacz z tego wspolczynniki a i b i napisz jak jest
postac wielomianu W(x)

