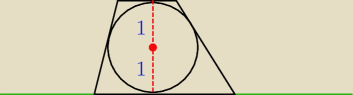
 i tak na pewno wysokość to 2.
i tak na pewno wysokość to 2.

 Tutaj wystarczy poprowadzić dwie wysokości z wierzchołków i powstają dwa proste trójkąty. Jeden
o kątach 45o 45o 90o.
Drugi o kątach 30o 60o 90o.
P.S. Ramię długości 2? Tyle ma wysokość. To oznacza że wysokość jest równa ramieniu?
Ramiona to:
2√2 oraz 4
teraz twierdzenie o okręgu wpisanym w czworokąt : a + b = c+d gdzie a i b to podstawy a c i d
to ramiona
teraz długość odcinka łączącego środki ramion:
Tutaj wystarczy poprowadzić dwie wysokości z wierzchołków i powstają dwa proste trójkąty. Jeden
o kątach 45o 45o 90o.
Drugi o kątach 30o 60o 90o.
P.S. Ramię długości 2? Tyle ma wysokość. To oznacza że wysokość jest równa ramieniu?
Ramiona to:
2√2 oraz 4
teraz twierdzenie o okręgu wpisanym w czworokąt : a + b = c+d gdzie a i b to podstawy a c i d
to ramiona
teraz długość odcinka łączącego środki ramion:
| a+b | c+d | ||
skoro a+b = c+d możemy to zapisać również | |||
| 2 | 2 |
| 2(√2+2) | |
= 2 + √2 | |
| 2 |
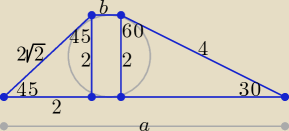 Korzystając z własności trójkąta prostokątnego o kącie ostrym 30o i trójkąta prostokątnego
o kącie ostrym 45o otrzymujemy długości ramion: 2√2 oraz 4.
Okrąg jest wpisany w czworokąt, więc a + b = 4 + 2√2
Korzystając z własności trójkąta prostokątnego o kącie ostrym 30o i trójkąta prostokątnego
o kącie ostrym 45o otrzymujemy długości ramion: 2√2 oraz 4.
Okrąg jest wpisany w czworokąt, więc a + b = 4 + 2√2
| a + b | 4 + 2√2 | |||
Długość odcinka łączącego środki ramion jest równa | = | = 2 + √2 | ||
| 2 | 2 |