długość boków trójkąta roman: Długość boków trójkąta są równe 3, 5, 2√7 a) określ rodzaj trójkąta ze względu na kąty b) oblicz długość promienia okręgu opisanego na tym trójkącie.

Ktoś: Tu masz o tym: http://www.matematyka.pl/256035.htm#p965098

ICSP: twierdzenie sinusów i cosinusów. Cosinusami sprawdzasz jaki to jest trójkąt. Jeżeli cos kata naprzeciw najdłuższego boku będzie ujemny znaczy to że trójkąt jest rozwartokątny.

roman: nie wiem czy dobrze to zrobilem najdluzszy bok wyszedl mi 2√7 , oznaczyłem go jako a, pozostale boki b i c. obliczylem cosy ze wzoru a² + b² − c² / 2ab, wynik w przyblizeniu 0,15. cosB 0,04. Jeśli to jest poprawne rozwiązanie to jest to trójkąt ostrokątny ?

ICSP: boki : 3 = 3 5 = 5 2√7 ≈ 5,29175026 3² + 5² − 2 * 3 * 5 * cosy = 4 * 7 9 + 25 − 30cosy = 28 −30cosy = −6 cosy = 0,2 czyli jest ostrokątny.

ICSP: masz do tego odpowiedzi? Mi promień wyszedł dziwny:

	5√42
R =
	2

ICSP: przepraszam 1 w mianowniku zgubiłem

	5√42
R =
	12

roman: Niestety nie, a z jakiego wzoru obliczyłeś promień ?

ICSP: z takiego:

	a		b		c
2R =		=		=
	sinα		sinβ		sinγ

Niestety nie odnosi się do tego że źle policzyłem czy do tego że nie masz odpowiedzi?

roman: że nie mam odpowiedzi, a można skorzystać np. z P = p * r gdzie p jest polowa obwodu trojkata?

ICSP: można ale skoro już liczyłeś tego cosinusa to go wykorzystaj. Właśnie tak są układane zadania.

ICSP: No i oczywiście trzeba jeszcze wiedzieć że wzór P = pr odnosi się do okręgu wpisanego w trójkąt a nie do opisanego.

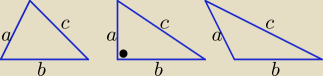
Bogdan: a² + b² > c² to trójkąt ostrokątny a² + b² = c² to trójkąt prostokątny a + b² < c² to trójkąt rozwartokątny −−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−− a = 3, b = 5, c = 2√7,

	1
p =		(3 + 5 + 2√7 = 4 + √7, p−a = √7 + 1, p−b = √7 − 1, p−c = 4 − √7
	2

Pole trójkąta z wzoru Herona: P_Δ = √ p*(p − a)*(p − b)*(p − c) = √9 * 6 = 3√6

	a*b*c
Długość promienia okręgu opisanego R =
	4*PΔ