:P:P ICSP: Eta posiadasz może kilka ciekawych zadań z planimetrii? Tylko takich z którymi sobie poradzę

Godzio: Etą nie jestem, ale mam zadanko Wyznaczyć promień okręgu opisanego na czworokącie ABCD, w którym kąt przy wierzchołku A ma miarę α, kąty przy wierzchołkach B, D są proste oraz |BC| = a, |AD| = b.

ICSP: najgorszy rodzaj zadania jaki tylko może być, ale właśnie taki powinienem robić.

Godzio: Chyba chciałeś powiedzieć najfajniejszy

ICSP: właśnie nie. Nie potrafię robić takich zadań:(. Na razie mam coś takiego: |AC| jest średnicą. Myślę czy nie trzeba tutaj czegoś z twierdzenia sinusów kombinować.

Godzio: Kombinuj, rozwiązanie jest proste, chodź ja zrobiłem to takim sposobem "dookoła świata", że wyszło mi na ponad jedną kartkę A4

ICSP: powiedz mi AC nie jest dwusieczną kąta A i C?

Godzio: Nie

Eta: to może takie? zad2/ Dwa kwadraty takie,że jeden powstaje z drugiego przez obrót dookoła środka kwadratu o kąt 45^o, tworzą szesnastokąt w kształcie gwiazdy. Oblicz pole tego szesnastokąta wiedząc,że jego obwód równa się a.

ICSP: a nie mogą być takie zadania z liczbami

ICSP: bo co do zadanka Godzia to przez bół godziny doszedłem do tego zę b² + |DC|² = a² + |AB|²

ICSP: Eta o cos takiego chodzi? I czy te kwadraty są identyczne?

Godzio: Ameryki nie odkryłeś

ICSP: cicho Nie mam talentu do tego typu zadań. Doszedłem również do tego że sinus kąta na przeciw kata A jest taki sam jak kata A

M4ciek: Godziu na jaki idziesz kierunek na PW ?

Vax: To może coś ode mnie, niedawno robiłem takie ciekawe zadanko Okrąg o środku O wpisany w czworokąt wypukły ABCD jest styczny do boków AB, BC, CD, DA odpowiednio w punktach K, L, M, N, przy czym proste KL i MN przecinają się w punkcie S. Dowieść, że proste OS i BD są prostopadłe. Pozdrawiam.

Godzio: Na matmę, a na no co innego mogę iść Eta

	1
P = (5 + √2) *		a2 ?
	128

Godzio: Taaa od Vaxa to pewnie mega rzeźnia

M4ciek: Tylko tam składasz czy jeszcze gdzieś

ICSP: mi Wyszło

a2		√2
	+
32		64

ICSP: + U{√2}a}{64}

Godzio: Tylko tam

ICSP: Boże chwileczke u mnie w obliczeniach a*a = a ... Muszę poprawić.

M4ciek: Możliwe ,że się zetkniemy jak się dostanę

Godzio: A też na matmę idziesz ?

M4ciek: Na geodezję i kartografię , to od tego roku otwierają

Eta:

	a2
P=		(2+√2) [ j2]
	64

Magda: geodezja i kartografia to wiem, że jest na Wojskowej Akademii Techinicznej bo mam tam kumpelę

M4ciek: Na wielu uczelniach jest np. Na AGH−u czy Uniwersytecie Przyrodniczym we Wrocku

Godzio:

	a2
Albo robię głupi błąd, albo ma być		(3 + √2) hmmm
	64

Magda: M4cku strzeż się kartografii : D mam co prawda znajomych ale na geografii i mają równiez kartografię to rysunki przy uzyciu kartografu musza poprawiac 1324324 razy i siedzieć po nocach xD bo muszą byc z dokładnością do jakiejś części milimetra z tego co słyszałam : D

ICSP: dobrze moje rozumowanie: powstanie osmiokąt foremny(jego bok oznaczamy jako x) oraz 8 identycznych trójkątów(ich boki oznaczamy jako y) 16y = a

	a
y =
	16

ponieważ x jest przekątną kwadratu o boku y możemy go wyrazić następująco

	a√2
x =
	16

Teraz pole tej figury to będzie pole dużego kwadratu i 4 mniejszych kwadratów:

	1
P = 4 *		* y2 + (x+2y)2 = 2y2 + x2 + 4xy + 4y2 = 6y2 + 4xy + x2
	2

Podstawiamy:

a2

a√2

a

a2

3a2

a2√2

P = 6 *

+ 4 *

*

+

=

+

256

16

16

128

128

64

	a2		4a2		a2√2		2a2 + √2a2
+		=		+		=
	128		128		64		64

Gdzie robie błąd skoro wynik to

	1
(5+√2) *		a2
	128

ICSP: Godziu... Jak mogłeś mnie tak zmylić:( Ja myślałem że tamto Eta napisła

Godzio: Czyli jednak ja nie umiem liczyć

ICSP: Vax a jesteś jeszcze w tym temacie bo bym miał sprawę

Vax: Tak jestem jeszcze

ICSP: słyszałeś kiedyś o metodzie itteracyjnej?

Eta: I ok

	2a2+a2√2		a2
P=		=		(2+√2)
	64		64

Vax: Szczerze mówiąc nie, jednak jak chcesz mogę Ci podać nr gg osoby która to powinna znać, jbc podaj swoje gg to Ci wyślę numer Pozdrawiam.

ICSP: to teraz Eta może ty rozwiążesz to zadanko Godzia? Ja sobie z nim niestety nie poradzę:(

ICSP: nie trzeba Znam 5 metod rozwiązywania układów to przeżyję bez tej jednej

Godzio: W takim razie podam rozwiązanie:

	b
cosβ =		⇒ sinβ = √1 − b2/x2
	x

	a
sin(α − β) =		= sinαcosβ − cosαsinβ
	x

a		b
	= sinα *		− √1 − b2/x2cosα /*x
x		x

a = bsinα − √x² − b²cosα √x² − b²cosα = bsinα − a /²

	b2sin2α − 2absinα + a2 + b2cos2α
x2 =
	cos2α

	a2 + b2 − 2absinα
x2 =
	cos2α

	√a2 + b2 − 2absinα
x =
	|cosα|

	1		1	√a2 + b2 − 2absinα
Czyli R =		x =
	2		2	|cosα|

ICSP: Ja to miałem rozwiązać? To jest proste? Jak ja z matury podstawowej nie mogłem zrobić zadania z wykazywaniem i gdyby nie Eta to bym go nie zrobił

Godzio: Ja tam robiłem to z tw. cosinusów w trójkącie: ABD i BCD, a dalej z tw. sinusów, więc tak po chłopsku można było robić

ziomek: jak wam się nudzi spróbujcie rozwiązać to: 1.Środek okręgu wpisanego w trapez prostokątny znajduje się w odległości 6 i 8 jednostek od końców ramienia pochyłego względem podstawy. Wyznacz pole trapezu.

	R
2.W wycinek koła o promieniu R wpisano okrąg o promieniu		. Oblicz pole wycinka koła.
	3

ICSP: ziomek masz do tego odpowiedzi?

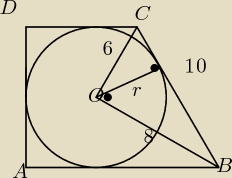
Vax: 1) Na początku zauważmy, że kąt BOC = 90*, z tw. Pitagorasa liczymy |BC| = 10, wysokość

	1
opuszczona na przeciwprostokątną jest promieniem okręgu, PBOC = 6*8*		= 24 ale z
	2

	1
drugiej strony 24 = PBOC = 10*r*		= 5r ⇔ r=4.8
	2

Teraz zauważmy, że (|AD| = 2r):

	(|AB|+|CD|)*h		(10+2r)*2r
PABCD =		=		= r(10+2r) = 4.8*19.6 = 94.08
	2		2

Pozdrawiam.

ICSP: Vax a mógłbyś jeszcze wytłumaczyć dlaczego BOC jest kątem prostym? Ja to policzyłem troszeczkę inaczej ale wyszło tak samo.

Vax: Zauważ, że suma miar kątów przy jednym ramieniu w trapezie wynosi 180*, niech kąt DCB = α , kąt CBA = β, czyli α+β = 180*, ale |CO| i |BO| to dwusieczne tych kątów, czyli kąt OCB + kąt CBO =

	α		β
		+		= 90* skąd wynika, że kąt BOC = 90*
	2		2

Pozdrawiam.

ICSP:

	1
co do drugiego to kompletnie strzelam że P =		R2π
	6

ICSP: Teraz już rozumiem Ja skorzystałem z tych deltoidów i ułożyłem układ równań z trzema niewiadomymi: x² + z² = 36 x² + y² = 64 x² = yz Po rozwiązanie wychodzi tak samo Oczywiście jestem bardzo wdzięczny za wytłumaczenie Pozdrawiam.

ICSP: Zrobi ktoś to drugie?

Eta:

	R
r=
	3

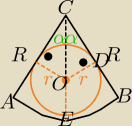
ΔODC jest prostokątny

	r
sinα=
	R−r

	1
sinα=............. =
	2

2α= 60^o policz teraz P_w=...........

ICSP:

	60		1
Pw =		* π * R2 =		R2π ?
	360		6

ziomek: sorry że tak późno, odpowiedzi są takie jak któreś z was było ciekawe :

	πR2A		πR2
P=		⇒P=
	360		6

i to jest odpowiedz do zadania 2. do zad 1 nie posiadam odp, ale pewnie dobrze jest Jak ktoś chce to wrzucę kilka kolejnych zadań , wystarczy poprosić

ICSP: wrzucaj śmiało Posimy

ICSP: Prosimy*

Godzio: A mojego nikt nie chciał rozwiązać:(

ICSP: którego twojego?

Godzio: https://matematykaszkolna.pl/forum/96523.html

ziomek: umiesz całki? Jak coś to mów nie będę takich dawać: ( mam do nich odp ale dam jak zrobicie , nie będę psuć zabawy ) trudne: 1.Obliczyć objętość bryły powstałej z obrotu wokól osi OX krzywej f(x)=2e^2x dla x∊<1,2>

	1		1
2.dla jakich wartości parametru A funkcja y=x2+xtgA+		tgA−		ma najmniejszą wartość
	2		4

	1		n2+3n+2
równą granicy ciągu an=(1−		n)ln		?
	4		n2+2n

łatwe: 1.Do windy wsiadło 5 pasażerów, budynek z tą windą liczy 10 pięter. Na ile sposobów mogą tę windę opuścić jeżeli każda z nich wysiada na innym piętrze 2.Oblicz szanse na główną wygraną w totka głównej wygranej. Gra polega na losowaniu 6 liczb z 49 (1,2...49)

ICSP: Całek nie umiem dopiero co liceum skończyłem, a prawdopodobieństwa nie ruszam, jedyna moja jedynka przez całe trzy lata nauki była z tego głupiego prawdopodobieństwa.

ziomek: aha to Godzio rozwiąże w sam raz dla niego ,zaraz coś znajdę bez całek/prawdopodobieństwa.

Godzio: 1. π₁²∫4e^4xdx = π (e^4x)|²₁ = π * (e^8x − e^4x) 2.

	n + 1		1		14
limn→∞ln(		)1 − n/4 = limn→∞ln(1 +		)*1/(1 +		)n/4
	n		n		n/4

	1		14		1
limn→∞ln(1 +		)*(1 +		)−n/4 → ln[1 * e−1/4] = −
	n		n/4		4

	−tg2A + 2tgA − 1		1		1
q =		= −		⇒ (tgA − 1)2 =
	2		4		2

	2 + √2		2 − √2
tgA =		lub tgA =
	2		2

	2 + √2		2 − √2
A = arctg		lub A = arctg
	2		2

Chyba dobrze, ale głowy nie dam

ziomek: 1.Objętość prostopadłościanu wynosi 216. Długości krawędzi są wyrazami ciągu geometrycznego i suma ich wynosi 21 znajdz długość krawędzi prostopadłościanu 2.Wykaż że stosunek objętości stożka do objętości kuli wpisanej w ten stożek jest równy stosunkowi pola powierzchni całkowitej stożka do pola powierzchni kuli. 3.wyznacz te wartości parametru a, dla których nierównośc kwadratowa (a²+4a−5)x²−2(a−1)x+2>0 jest spełniona dla wszystkich x∊R

ICSP: Te już ładniej wyglądają. Na pewno się dziś nimi zajmę

ICSP: Co do pierwszego: 3,6,12 ?

ICSP: 216 = abc a+b+c = 21 b² = ac 216 = b³ b = 6 a + c = 15

	36
36 = ac ⇔ a =
	c

36
	+c = 15
c

c² − 15c + 36 = 0 Δ = 81 c₁ = 3 c₂ =12 Czyli 3,6,12

ziomek: 1 do tego zadania z całkami b.dobrze Godzio. Wszystko jak należy 2. do tego z liczeniem parametru "A" zrobili na 3 różne sposoby chyba, ale żadne rozw. podobne do tego. Później to przepisze/zeskanuje bo dość długie jest.( co nie oznacza że zrobiłeś źle, ktos najwyżej sprawdzi Twoje rozwiązanie)

ziomek: ICSP, tu tak zrobili że skoro dł. krawędzi tworzą ciąg geometryczny to można oznaczyć a,aq,aq² i z warunku a>0 i q>0 zapisali układ : a³q³=216 a+aq+aq²=21 policzyli że q=2 lub q=1/2 i wyszło im że a=3 ⇔3,6,12 lub a =12 ⇔12,6,3 i takie były dł. krawędzi

ICSP: no to identycznie mi wyszło tylko inaczej rozwiązałem.

Godzio:

	−Δ
Dobra q =		ja dałem 2 ...
	4a

Poprawka zaraz będzie

Godzio:

	−tg2A + 2tgA − 1		1
q =		= −		⇒ (tgA − 1)2 = 1 ⇒
	4		4

tgA − 1 = 1 lub tgA − 1 = − 1 tgA = 2 lub tgA = 0 A = arctg2 + kπ lub A = kπ

ziomek:

	1
teraz to jest podobne do rozwiązania w książce ale oni dali od momentu =−		⇔−tg2A+2tgA=0
	4

tgA=0 lub tgA=2 a=kπ lub A=B+kπ, gdzie B jest takim kątem dla którego tgB=2