PC=90CM2 8A+4H=48 A=? H=? NICK:

^^: P_c = 90 8a + 4H = 48 czyli chodzi o graniastosłup prawidłowy trójkątny

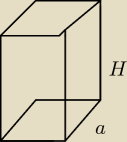
jhk: P_c = 2 * a² + 4 * ah = 90 8a + 4H = 48 mamy układ równań. sprubujmy z drugiego równania wyznaczyć H mamy 2a² + 4aH = 90 H = 12 − 2a i teraz podstawiamy 2 równanie do pierwszego. 2a² + 4a(12 − 2a) = 90 H = 12 − 2a 2a²+ 48a − 8a² = 90 H = 12 − 2a −6a² + 48a − 90 = 0 / dzielone na 6 H = 12 − 2a −a² + 8a − 15 = 0 H = 12 − 2a założenia jakie mamy a>0 oraz H>0 ponieważ sa to długości więc muszą być większe od zera. rozwiązujemy pierwsze równanie kwadratowe. Δ = 64 − 60 = 4 √Δ = 2 a₁ = ⁻⁸⁺²₋₂ = 3 a₂ = ⁻⁸⁻²₋₂ = 5 obie wartości "a" są większe od zeraz czyli wygląda na to ze mamy dwie możliwości, trzeba jeszcze tylko wyznaczyć wartości H −−−−−> H = 12 − 2a H₁ = 12 − 2*3 = 6 H₂ = 12 − 2*5 = 2 czyli dwie możliwości wyszły nam takie. albo a=3 i H = 6 lub a = 5 i H = 2