Kąty
Godzio: rumpek − kąty 
Trochę szybciej niż zapowiadałem
Kąty zaznaczaj na figurach przestrzennych które mają w podstawie
trójkąt lub czworokąt
może być foremny [ to na czerwono chce żeby był trójkąt ]
Narysuj kąt:
a) W graniastosłupie:
−
między ścianami bocznymi
−
między przekątną ściany bocznej, a sąsiednią ścianą boczną
− między przekątnymi sąsiednich ścian bocznych
− między przekątną ściany bocznej, a płaszczyzną podstawy
b) W ostrosłupie:
− między ścianami bocznymi
− nachylenia ściany bocznej do płaszczyzny podstawy
− nachylenia krawędzi bocznej do płaszczyzny podstawy
Dodatkowo, gdzie leży spodek wysokości w ostrosłupie jeśli:
a) wszystkie krawędzie są równe lub padają pod tym samym kątem na płaszczyznę podstawy
b) wszystkie ściany boczne są nachylone do płaszczyzny podstawy pod tym samym kątem
9 cze 23:18
rumpek:
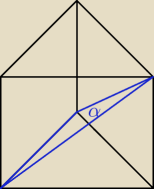
a) Graniastosłup
− między ścianami bocznymi − przy nim w graniastosłupie mam najwięcej wątpliwości
Rysunek powyżej

9 cze 23:38
Godzio:
Źle, próbuj dalej

9 cze 23:38
Godzio: A przy okazji możesz powiedzieć co to za kąt zaznaczyłeś

9 cze 23:39
rumpek: Kąt między przekątnymi ścian bocznych ?

9 cze 23:39
Godzio:
Tak

9 cze 23:40
rumpek:
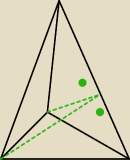
To może wyjdźmy od czegoś czego wiem:
To w ostrosłupie − dwuścienny tak zwany − między ścianami bocznymi, tak

?
9 cze 23:42
Godzio:
Ok

9 cze 23:48
rumpek:
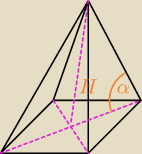
−nachylenia ściany bocznej do płaszczyzny podstawy :
Tak czy nie tak

?
9 cze 23:55
Godzio:
Nie
10 cze 00:10
rumpek: To to co narysowałem to jest kąt między ścianą boczną z podstawą? Czy jaki
10 cze 00:12
Godzio:
Przeczytaj to co napisałeś

10 cze 00:13
rumpek:
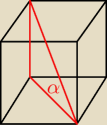
Właśnie mi się to myli przykład wyżej − narysowałem kąt między przekątną a podstawą w
sześcianie (chociaż łatwiej idzie napisać kąt między przekątną a przekątną podstawy )
10 cze 00:16
Godzio:
Kąt jest ok
10 cze 00:17
rumpek:
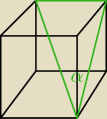
Kąt między przekątną a ścianą boczną w sześcianie
10 cze 00:19
Godzio: To jest kąt między przekątną sześcianu, a przekątną ściany bocznej
10 cze 00:20
rumpek: A na pewno nie kąt między przekątną a ścianą boczną w sześcianie?
10 cze 00:21
Godzio:
Tak

10 cze 00:21
10 cze 00:21
Godzio:
Przekątną ściany bocznej oczywiście

10 cze 00:22
Godzio:
Naczy to jest dobrze, ale mi chodzi o bardziej nietypowy kąt
10 cze 00:23
rumpek: 
10 cze 00:23
rumpek: A w graniastosłupie kąt między ścianami bocznymi będzie podobny trochę do tego z ostrosłupa

?
10 cze 00:24
Godzio:
Wiesz co, ja już będę lecieć, a Ty sobie porysuj te kąty, jutro je sprawdzę
Dobranoc

10 cze 00:24
Godzio:
Nie

To jest taki kąt który zawsze się myli, a jest najprostszy

10 cze 00:25
rumpek: Też już będę leciał

Jutro mam cały dzień na kąty

A po kątach do prostych rachunków
i na końcu rzeźnia

10 cze 00:25
rumpek:
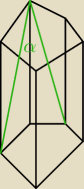
Takie pytanie: to wyżej to jest kąt między ścianami bocznymi w graniastosłupie, tak? Sorki, że
taki krzywy

10 cze 14:50
Godzio:
Nie

10 cze 15:18
ICSP: kąt między sąsiednimi ścianami bocznymi?
10 cze 15:19
Godzio:
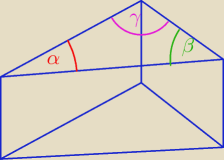
A to nie są kąty między ścianami bocznymi

?
10 cze 15:21
ICSP: kat między przekątnymi sąsiednich ścian bocznych w graniastosłupie?
10 cze 15:22
Godzio:
Tamten co narysowałeś tak, ale ten kąt już rysowałeś
10 cze 15:23
ICSP: haha mam cie, nie jestem rumpek

10 cze 15:24
Godzio: hah

nawet się nie skapnąłem
10 cze 15:25
10 cze 15:27
rumpek:
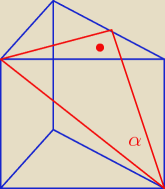
między przekątną ściany bocznej a ściany bocznej i teraz pytanie czy to trochę podobne jest do
kąta między ścianami bocznymi ?

10 cze 15:32
rumpek:
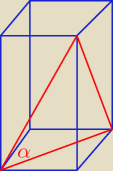
między przekątną ściany bocznej a podstawą
10 cze 16:00
Godzio:
Jest ok
10 cze 16:08
rumpek: Oba

?
10 cze 16:11
rumpek: p.s. to miał być kąt między przekątną ściany bocznej a płaszczyzną podstawy − więc chyba tak
jak narysowałem

, tak?
10 cze 16:12
Godzio: Tak,
10 cze 16:31
rumpek:
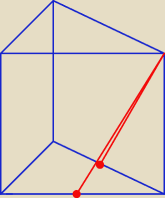
Zaryzykuje − ten kąt to ten między sąsiednimi sianami bocznymi

?
10 cze 16:37
rumpek: Czy jakoś inaczej?
10 cze 16:41
Godzio:
Ten kąt już rysowałem, zobacz wyżej
10 cze 16:42
rumpek: Aaaaaaaaaaa

to tak wygląda myślałem, że rysować jakieś takie

a tu najprostsze jakie może być xD
10 cze 16:43
Godzio: 
10 cze 16:44
rumpek: Czyli graniastosłupy zakończone

Trzeba dokończyć ostrosłupy

10 cze 16:44
rumpek:
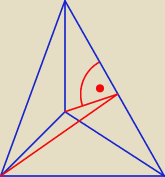
To ten co już rysowałem − między ścianami bocznymi tak zwany dwuścienny

10 cze 16:48
rumpek:
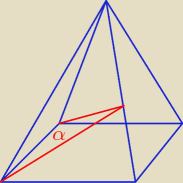
A taki może być "między ścianami bocznymi" o podstawie czworokątu?
10 cze 16:50
rumpek: A kąt między przekątną ściany bocznej, a sąsiednią ścianą boczną można narysować w
graniastosłupie o podstawie czworokąta?

10 cze 16:54
Godzio:
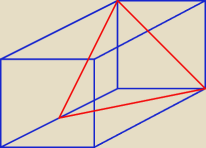
To raczej nie jest ten kąt "między ścianami bocznymi"
Co do pytania, to chyba będzie taki kąt
10 cze 17:14
ICSP: ale kata nie zaznaczyłeś:(
10 cze 17:15
rumpek: A jaki jest kąt dwuścienny w ostrosłupie o podstawie czworokąta? Bo to co narysowałeś to
chyba to o co pytalem − między ścianą boczną a przekątną ściany bocznej

10 cze 17:18
rumpek: Już wiem

10 cze 17:19
ICSP:
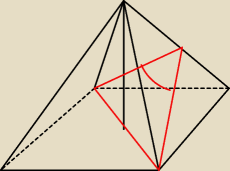
10 cze 17:19
rumpek:
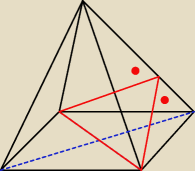

10 cze 17:20
rumpek:
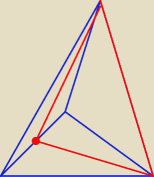
A jak w ostrosłupie narysować kąt między ścianą boczną a przekątną ściany bocznej. Tak o?
10 cze 17:27
Godzio:
Zastanów się, czy istnieje coś takiego jak przekątna ściany bocznej w ostrosłupie

10 cze 17:52
rumpek: no właśnie chyba nie

i to była największa wątpliwość xD
10 cze 17:54
rumpek:
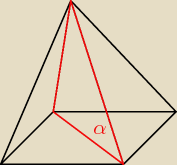
nachylenie krawędzi bocznej do płaszczyzny podstawy
10 cze 17:58
Godzio:
Ok

10 cze 18:12
rumpek:
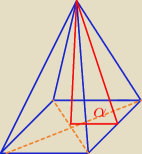
kąt nachylenia ściany bocznej do płaszczyzny podstawy = coś takiego?
10 cze 18:22
Godzio:
Tak
10 cze 18:28
rumpek:

śmigam na rower, potem dokończę rysowanie tych wysokości bodajże

bo tylko one
zostały. Więcej kątów nie ma, które mogą pojawić się w zadaniach?
10 cze 18:30
Godzio:
Raczej nie

10 cze 18:44
rumpek: a) wszystkie krawędzie są równe lub padają pod tym samym kątem na płaszczyznę podstawy
czyli wszystkie tak zwane długości a są równe, tak? Jeżeli tak to jest to czworościan foremny,
tak

?
10 cze 21:14
Godzio:
Sorry, krawędzie boczne miało być oczywiście

10 cze 21:14
rumpek:
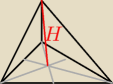
ale jak wszystkie krawędzie są równe, to jest to czworościan foremny tak

? I wysokość na
rysunku wyżejY
10 cze 21:18
Godzio:
Tak, jak mamy ostrosłup prawidłowy to spodkiem wysokości jest zawsze ten sam

10 cze 21:19
rumpek: A odnośnie tego, że wszystkie ściany boczne są równe, więc podstawa jest inna.
Myślę, że jest to ostrosłup prawidłowy trójkątny, tak? Wtedy jego boki są trójkątami
równoramiennymi

10 cze 21:19
Godzio: ten sam punkt (nie dopisałem

)
10 cze 21:19
rumpek:
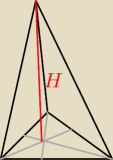

10 cze 21:20
Godzio:
Tu nie o to chodzi, podstawa jest dowolna,
Podam Ci to żeby już się nie bawić, tylko postaraj się to zapamiętać:
a) Jeśli wszystkie ściany boczne ostrosłupa tworzą z podstawą równe kąty lub jeśli
wysokości wszystkich ścian bocznych, poprowadzone z wierzchołka ostrosłupa,
są równe, to w podstawę ostrosłupa można wpisać okrąg, a środkiem tego okręgu
jest spodek wysokości ostrosłupa.
b) Jeśli wszystkie krawędzie boczne ostrosłupa są równe lub jeśli wszystkie krawędzie
boczne tworzą z płaszczyzną podstawy równe kąty, to na podstawie ostrosłupa można
opisać okrąg, a środkiem tego okręgu jest spodek wysokości ostrosłupa.
10 cze 21:20
rumpek:
b) wszystkie ściany boczne są nachylone do płaszczyzny podstawy pod tym samym kątem
jest jakaś różnica między tamtym?
10 cze 21:21
rumpek:
aha ok, dzięki

teraz powtórzyć wzory i za niedługo poproszę o jakieś proste zadania

a po
prostych do rzeźniczych

10 cze 21:23
rumpek:
 Godzio
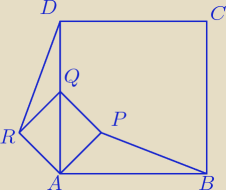
Godzio mam takie pytanie odnośnie takiego zadania:
trzeba udowodnić, że |BP| = |DR| a APQR i ABCD są kwadratami.
To skleiłem coś takiego:
na podstawie przystawania (
bkb) trójkątów: ABP i ADR
1
o Kwadrat ABCD ma wszystkie boki równe, więc podstawy trójkątów (ABP i ADR ) są równe:
|AB| = |AD|
2
o Kwadrat APQR masz wszystkie boki równe, więc boki trójkątów (ABP i ADR) są równe:
|AP| = |AR|
3
o Każdy kwadrat masz 4 kąty proste (4 * 90
o = 360
o). Przy każdym wierzchołku ma kąt 90
o,
więc: w kwadracie ABCD mamy: ∡DAP = 90
o − ∡BAP, natomiast w kwadracie APQR mamy:
∡DAR = 90
o − ∡DAP ⇒ ∡DAR = 90
o − (90
o − ∡BAP) ⇒∡DAR = ∡BAP. Więc kąty są równe.
Na podstawie przystawania trójkątów wykazałem, iż odcinki |BP| i |DR| są równej długości.
c.n.u.

12 cze 19:18
Godzio:
Perfekcyjnie udowodnione

12 cze 20:03
rumpek: 
12 cze 20:10
rumpek: Godzio rozumiesz dobrze kombinatorykę

?
22 cze 15:07
Godzio:
Nie specjalnie

22 cze 16:22
rumpek: A rozróżniasz kiedy ta kombinacja a wariacje?

22 cze 16:43
rumpek: A mógłbyś przygotować mi jakieś łatwy zestaw z "reguły mnożenia". Bo wypadałoby zacząć
naukę od podstaw, a kombinatoryka i prawdopodobieństwo to nie są za łatwe działy

22 cze 17:18
rumpek: Podbijam

22 cze 18:31
Godzio:
Teraz nie mam za bardzo kiedy, jakiegoś dnia się pomyśli

22 cze 18:32
rumpek: oki, thx
22 cze 18:33
ziomek: masz rumpek zadania:
1.Tinky Winky ma trzy torebki−
czerwoną,
zieloną,
niebieską, do torebek zamierza
włożyć cztery różne zdjęcia pani Ewy.
a)Na ile sposobów Tinky Winky może rozmieścić zdjęcia w swoich torebkach
b)Na ile sposobów może rozmieścić zdjęcia tak ,aby w czerwonej torebce nie znalazło się żadne
zdjęcie
c)Na ile sposobów może rozmieścić zdjęcia tak ,aby w czerwonej torebce nie znalazło się żadne
zdjęcie, a w niebieskiej i żółtej co najmniej jedno?
d) Na ile sposobów może rozmieścić zdjęcia tak, aby w każdej torebce znalazło się co najmniej
jedno zdjęcie.
2.Używając cyfr ze zbioru {o,1,2,3,4,5} zapisujemy liczby czterocyfrowe (cyfry w liczbie nie
mogą się powtarzać)Oblicz, ile możemy zapisać:
a)liczb czterocyfrowych
b)liczb większych od 4999
c)takich liczb,że suma tysięcy i cyfra dziesiątek jest nieparzysta ,a pozostałe dwie są
parzyste.
d)liczb podzielnych przez 5.
Co do rozróżniania kombinacji i wariacji...
kombinacja gdy kolejność nie jest istotna np :
a)na ile sposobów można wylosować pięć kart z talii 52?
Oraz dla liceum jest tylko kombinacja bez powtórzeń.Nie ma wzoru na tą z powtórzeniami(tzn w
programie dla poz. rozszerzonego)
wariacja gdy kolejność jest ważna np dla czegoś co tworzy ciąg, pamiętasz pewnie że w ciągach
kolejność wyrazów odgrywała role to podobnie tu, np:
masz policzyć
A) ile jest liczb pięciocyfrowych w których
−cyfry nie mogą się powtarzać
−cyfry mogą się powtarzać
Jest wzór na wariacje z powtórzeniami i bez
| | n! | |
oraz permutacja jeżeli po podstawieniu do wzoru na wariacje Vnk= |
| ! wyjdzie Ci że n=k |
| | n−k | |
Generalnie lepiej robi się tymi wzorami zadania, niżeli jakimiś pieprzonymi drzewkami

Przynajmniej mniej roboty i nie musisz nic rysować.
22 cze 21:18
ziomek: zad 2 możesz zrobić w takiej samej formie ale gdy cyfry mogą się powtarzać
22 cze 21:24
ziomek: | | n! | |
i we wzorze na wariacje miało być Vnk= |
| |
| | (n−k)! | |
22 cze 21:27
M4ciek:
Widzę zadania z Kiełbasy
ziomek 
23 cze 11:31
rumpek:
Zadanie 2 (różne liczby)
a) ile jest liczb czterocyfrowych? − Na podstawie zbioru {0,1,2,3,4,5} mamy:
− − − −
1 2 3 4
Pierwszą liczbę mogę wybrać ze zbioru {1,2,3,4,5} jest on 5cio elementowy (5).
Drugą liczbę mogę wybrać ze zbioru {0,1,2,3,4,5} jest on 6cio elementowy, trzeba pamiętać o
odjęciu jednej liczby i mam do wyboru również (5) liczb
Trzecią liczbę mogę wybrać ze zbioru {0,1,2,3,4,5} jest on 6cio elementowy i również zabieram
dwie liczby (bo już dwie wykorzystałem) i zostaje (4) liczb
Czwartą liczbę mogę wybrać ze zbioru {0,1,2,3,4,5} tylko na 3 sposoby.
Co daje:
5 * 5 * 4 * 3 =
300 sposobów
b) liczb większych od 4999
− − − −
1 2 3 4
Pierwszą liczbę mogę wybrać tylko na jeden sposób − tylko liczba 5 spełnia to, ponieważ nie mam
w zbiorze żadnej dziewiątki.
Drugą liczbę mogę wybrać na 5 sposobów (o jeden mniej bo już wybrałem jedną liczbę)
Trzecią liczbę mogę wybrać na 4 sposoby (o dwie mniej bo już zostały wybrane)
Czwartą liczbę mogę wybrać na 3 sposoby (o trzy mniej bo już zostały wybrane jakieś liczby)
Co daje:
1 * 5 * 4 * 3 =
60
c) takich liczb,że suma tysięcy i cyfra dziesiątek jest nieparzysta ,a pozostałe dwie są
parzyste
− − − −
1 2 3 4
Wpierw wypisze liczby parzyste i nieparzyste ze zbioru {0,1,2,3,4,5}
Parzyste: 1,3,5
Nieparzyste: 0,2,4
Pierwszą liczbę (tysiące − nieparzyste) mogę wybrać na 3 sposoby
Druga liczbę (setki − parzyste) mogę wybrać również na 3 sposoby
Trzecią liczbę (dziesiątki − nieparzyste) mogę wybrać na 2 sposoby (bo jedna już poszła na
tysiące)
Czwartą liczbę (jedności − parzyste) mogę wybrać na 2 sposoby (bo jedna już poszła na setki)
Co daje:
3 * 3 * 2 * 2 =
36
d) liczb podzielnych przez 5.
Liczba jest podzielna przez 5, gdy ostatnią cyfrą jest 0 lub 5 więc:
1
o 5
− − − −
1 2 3 4
ze zbioru {0,1,2,3,4,5}
Ostatnią (czwartą) cyfrę mogę wybrać tylko na jeden sposób − jest to piątka (5)
Pierwszą cyfrę mogę wybrać (nie mogę wziąć 0 bo to nie będzie liczba czterocyfrowa − jest
łącznie 6 liczb − jedna odchodzi (piątka) i zero wypada) więc tylko na 4 sposoby
Drugą cyfrę mogę wybrać na (zbiór 6cio elementowy dwie wykorzystałem) 4 sposoby
Trzecią cyfrę mogę wybrać na 3 sposoby
Co daje:
4 * 4 * 3 * 1 =
48
2
o 0
− − − −
1 2 3 4
Ostatnią liczbą jest 0 co nam ułatwia całą pracę (bo nie musimy go jako pierwszej uwzględniać)
Czyli:
Czwartą liczbę mogę wybrać na 1 sposobów.
Pierwszą liczbę mogę wybrać na 5 sposobów (0 już wybrałem więc zmniejszam o jeden)
Drugą liczbę mogę wybrać na 4 sposoby (dwie liczby wykorzystane)
Trzecią liczbę mogę wybrać na 3 sposoby (trzy liczby już wykorzystane)
5 * 4 * 3 * 1 =
60
Podsumowując:
60 + 48 =
108 − tyle możliwości

23 cze 15:33
rumpek:
Zadanie 2 (te same liczby)
a)liczb czterocyfrowych
− − − −
1 2 3 4
Ze zbioru {0,1,2,3,4,5} tylko na 5 sposobów mogę wybrać pierwszą liczbę, pozostałe trzy liczby
mogę już wybrać na 6 sposobów.
Zatem:
5 * 6 * 6 * 6 = 1080
b)liczb większych od 4999
− − − −
1 2 3 4
Pierwszą liczbę mogę wybrać tylko na jeden sposób: może to być tylko 5. Reszta normalnie na 6
sposobów.
Zatem:
1 * 6 * 6 * 6 = 216
c)takich liczb,że suma tysięcy i cyfra dziesiątek jest nieparzysta ,a pozostałe dwie są
parzyste.
− − − −
1 2 3 4
Ze zbioru {0,1,2,3,4,5}
Tak jak poprzednio:
parzyste: 0,2,4
nieparzyste: 1,3,5
Tysiące i dziesiątki mogę wybrać ze zbioru {1,3,5}, więc po 3 sposoby
Podobnie setki i jedności: mogę wybrać ze zbioru {0,2,4} więc również po 3 sposoby
Zatem:
3 * 3 * 3 * 3 = 81
d)liczb podzielnych przez 5
Tak samo jak wyżej, dwa przypadki:
1o. Dla 0
− − − −
1 2 3 4
Ostatnią liczbę mogę wybrać na jeden sposób (tylko 0!), resztę liczb prócz pierwszej (bo nie
może być 0) mogę wybrać na 6 sposobów, więc:
5 * 6 * 6 * 1 = 180
2o Dla 5
− − − −
1 2 3 4
Ostatnią liczbę mogę wybrać na jeden sposób (jedynie 5) a resztę prócz pierwszej liczby (nie
może być 0) na 6 sposobów. I mamy:
5 * 6 * 6 * 1 = 180
Sumując:
180 + 180 = 360
23 cze 15:43
rumpek:
Zadanie 1
a)Na ile sposobów Tinky Winky może rozmieścić zdjęcia w swoich torebkach
Są trzy torebki i cztery zdjęcia. Dla każdego zdjęcia są trzy możliwości (albo do czerwonej
albo do zielonej lub do niebieskiej). A że są cztery zdjęcia to mamy:
3 * 3 * 3 * 3 =
81
b)Na ile sposobów może rozmieścić zdjęcia tak ,aby w czerwonej torebce nie znalazło się żadne
zdjęcie
To zostają na dwie torebki. Czyli tak jak wyżej robimy: jedno zdjęcie może włożyć albo do
zielonej albo do niebieskiej. A że są cztery zdjęcia więc mamy:
2 * 2 * 2 * 2 =
16
c)Na ile sposobów może rozmieścić zdjęcia tak ,aby w czerwonej torebce nie znalazło się żadne
zdjęcie, a w niebieskiej i żółtej co najmniej jedno?
(na pewno żółtej? a nie zielonej?)
Żeby nie było w czerwonej torebce mamy:
16, lecz w tych możliwościach są takie przypadki,
że wszystkie zdjęcia są w torebce niebieskiej, i wszystkie zdjęcia się w torebce zielonej. A
żeby nie było takich możliwości (bo mają być co najmniej jedno zdjęcie więc te dwie odpadają)
trzeba odjąć te dwie możliwości od 16 i otrzymamy
14
d) Na ile sposobów może rozmieścić zdjęcia tak, aby w każdej torebce znalazło się co najmniej
jedno zdjęcie.
Hmm

do tego podpunktu mam najwięcej wątpliwości ale zaryzykuję:
Wszystkich możliwości jest
81. Są trzy torebki:
1
o przypadek:
Gdy czerwona jest pusta, a w zielonej i niebieskiej jest co najmniej po jednym zdjęciu.
Wyliczyłem to wyżej jest takich możliwości 1.
2
o przypadek:
Gdy zielona jest pusta, a w czerwonej i niebieskiej jest co najmniej po jednym zdjęciu. Też
jest 14 (na podstawie przypadku pierwszego)
3
o przypadek:
Gdy niebieska jest pusta, a w czerwonej i zielonej jest co najmniej po jednym zdjęciu. Również
jest 14 (dwa przypadki wyżej)
Więc raczej:
81 − 14 * 3 =
81 − 42 = 39
Jednak jeszcze chyba trzeba sprawdzić kiedy wszystkie zdjęcia znajdują się w jednej torebce −
są trzy torebki więc są trzy możliwości.
Więc dodatkowo:
39 − 3 =
36
Z tym miałem najwięcej wątpliwości, proszę sprawdzić

I proszę o jeszcze jakieś zadania, ale w osobnym temacie, aby nie ciągnąć tego ze stereometrii
tak

thx
23 cze 16:02
ziomek: ok, da rade wezmę tym razem ze zbioru 2200 zadań z CKA. Mają ciekawsze z tego działu zadania ,
przy okazji zajrzę
do Kiełbasy czy wyniki się zgadzają, jutro 24 sprawdź kolo 13.00 to będziesz mieć w tym temacie
czy dobrze zrobiłeś i osobno w innym zadania z kombinatoryki.
23 cze 20:50
rumpek: Ale tylko z reguły mnożenia proszę

Bo na razie temu chcę czas poświęcić
 Godzio
Godzio
jakbyś miał już czas to jakimiś zadaniami nie pogardziłbym

23 cze 21:12
Godzio:
Jutro coś wsadzę koło 15−18
23 cze 21:22
rumpek: Dziękuję

23 cze 21:23
roman: ech rumpek ....
Wpierw wypisze liczby parzyste i nieparzyste ze zbioru {0,1,2,3,4,5}
Parzyste: 1,3,5
Nieparzyste: 0,2,4

24 cze 11:15
rumpek:
Jasny gwint

Parzyste: {0,2,4}
Nieparzyste: {1,3,5}
Sorki xD nieuwaga

24 cze 11:16
ziomek: zadanie z tinky winky
a) 34=81
b)24=16
c)16−2=14
d)od liczby wszystkich rozmieszczeń(81) musimy odjąć liczbę takich rozmieszczeń ,że dokładnie
jedna torebka jest pusta. Jest ich 3*14, oraz takich że wszystkie zdjęcia znajdą się w jednej
torebce (są takie 3 rozmieszczenia) zatem tinky winky może rozmieścić zdjęcia na 36 sposobów .
zad z liczbami czterocyfrowymi
z powtórzeniami
a)5*63=1080
b)1*63=216
c)34=81
d)5*6*6*2=360
bez powtórzeń
5*5*4*3=300
b)1*5*4*3=60
c)3*3*2*2=36
d)aby dzieliła się na 5 to jedność liczby ma wynosić 5 lub 0
jest 5! liczb o różnych cyfrach których cyfrą jedności jest 0 oraz 4*4*3*1 których cyfrą
jedności jest 5 czyli :
60+48=108
24 cze 13:10
rumpek: Nie łatwiej było napisać, że wszystko ok

?
24 cze 13:19
Godzio:
Zad. 1 W restauracji serwuje się 4 rodzaje zup, 8 drugich dań i 7 deserów. Ile różnych zestawów
obiadowych, składających się z zupy, drugiego dania i deseru można zamówić w tej restauracji?
Zad. 2 Na ile sposobów można posadzić na ławce 5 koleżanek , tak aby
a) siedziały obok siebie w dowolnej kolejności ,
b) dwie koleżanki Krysia i Iza siedziały obok siebie ?
Zad. 3 Na ile sposobów można ustawić w kolejce trójkę dziewcząt i trójkę chłopców tak , aby
dziewczęta i chłopcy stali na przemian.
Zad. 4 Ile różnych liczb 5 cyfrowych o niepowtarzających się cyfrach można utworzyć z cyfr : 0,
1, 2, 3, 4 ?
Zad. 5 ile jest liczb czterocyfrowych w których nie powtarza się żadna cyfra?
Zad. 6 Ile jest liczb nieparzystych trzycyfrowych liczb o różnych cyfrach?
Zad. 7 Ile jest liczb trzycyfrowych (cyfry mogą się powtarzać)
a)utworzonych z liczb parzystych ?
b)mniejszych od 700 i większych od 500?
Zad. 8 Ile można otrzymać wyników, rzucając: a) pięć razy monetą lub pięcioma monetami, b) dwa
razy kostką i trzy razy monetą?
Teraz zadania pisze z pamięci, takie typowe:
Zad. 9 Jest blok 8 piętrowy i 5 ludzi, na ile sposobów mogą wysiąść pasażerowie,
a) dowolnie
b) każdy na innym piętrze
Zad. 10 Jest 8 pudełek i 9 kul, na ile sposobów można umieścić kule w pudełkach
a) dowolnie
b) wszystkie znajdą się w różnych pudełkach
c) wszystkie kule znajdą się w 3 pudełkach
Zadania postaraj się zrobić w jednym poście, tak najłatwiej będzie mi to sprawdzić, sorki że
tak późno, trochę sobie pospałem

24 cze 18:24
rumpek:
Zad 1
4 rodzaje zup
8 drugich dań
7 deserów
4 * 8 * 7 =
224
Zad 2
Chyba mogę sobie zapisać tak: {D
1, D
2, D
3, D
4, D
5}
No i tam loszki mogę rozmieścić na sposobów:
D
1 − 5 sposobów
D
2 − 4 sposoby
D
3 − 3 sposoby
D
4 − 2 sposoby
D
1 − 1 sposób
czyli:
5 * 4 * 3 * 2 * 1 =
120 (5! − permutacja jak nic

)
b) (to to w ogóle permutacją zalatuje

− muszę o niej doczytać)
Jak to zrobić regułą mnożenia?
Zad 3
D
1 C
1 D
2 C
2 D
3 C
3
Dziewczyny = 3!
Chłopcy = 3!
6 * 6 =
36
C
1 D
1 C
2 D
2 C
3 D
3
Dziewczyny = 3!
Chłopcy = 3!
6 * 6 =
36
Sumując:
36 + 36 =
72
Zad 4
Ze zbioru {0,1,2,3,4}
− − − − −
1 2 3 4 5
Pierwsze miejsce mogę obsadzić na 4 sposoby (bez 0)
Drugie miejsce mogę obsadzić na 4 sposoby (bez pierwszej liczby)
Trzecie miejsce mogę wybrać na 3 sposoby (bez dwóch poprzednich)
Czwarte miejsce mogę wybrać na 2 sposoby (bez trzech poprzednich)
Ostatnie tylko na jeden sposób
4 * 4 * 3 * 2 * 1 =
96
Zad 5
Liczby to: {0,1,2,3,4,5,6,7,8,9} jest ich 10 więc:
− − − −
1 2 3 4
Pierwszą liczbę mogę wybrać na 9 sposobów
Drugą liczbę mogę wybrać na 9 sposobów
Trzecią liczbę mogę wybrać na 8 sposób
Czwartą liczbę mogę wybrać na 7 sposobów
Więc:
9 * 9 * 8 * 7 =
4536
Zad 6
Ze zbioru {0,1,2,3,4,5,6,7,8,9}
Nieparzysta liczba − na końcu liczby nie parzyste więc: {1,3,5,7,9} − jest ich 5
Więc:
− − −
1 2 3
Ostatnią liczbę mogę wybrać na 5 sposobów.
Pierwszą liczbę mogę wybrać na 8 sposobów
Drugą liczbę mogę wybrać na 8 sposobów
8 * 8 * 5 =
320
Zad 7
a)
Ze zbioru {0,1,2,3,4,5,6,7,8,9} wybieram parzyste i mam:
{0,2,4,6,8} − 8 możliwości
− − −
1 2 3
Ma być trzycyfrowa liczba więc mogę ją wybrać na: (mogą się powtarzać)
4 * 5 * 5 =
100
b)
− − −
1 2 3
Pierwszą mogę wybrać tylko {5,6} czyli na dwa sposoby
Druga mogę wybrać na 10 sposobów
Trzecią na też na 10 sposobów.
2 * 10 * 10 =
200 (odejmuję jedną bo może być ułożenie 500

)
200 −
1 =
199 i mamy odpowiedź

Zad 8 9 i 10
to na pewno da się zrobić
regułą mnożenia? bo tylko o takie na razie zadanka prosiłem

24 cze 22:37
Eta:
zad 2 b)
K I x x x
x K I x x
x x K I x
x x x K I
(Krysia , Iza ) , ( Iza, Krysia) na 2! sposobów na czterech pozycjach w danej piatce
pozostałe trzy osoby (x,x,x) na 3! sposobów
i mamy: 2!*4*3!=.......... sposobów

24 cze 22:51
rumpek:
Ajajajaj

zapomniałem, że Krysia i Iza też mogą się zamienić stronami

2! − wiem skąd
3! − wiem skąd
4 − nie do końca wiem (czyżby z tego, że są cztery przypadki?)

Dziękuje

(reszta dobrze?)
24 cze 23:02
Godzio:
Może czegoś tam z reguły nie dałem

Zadania sprawdzę jutro wieczorem, chyba że
Eta to już zrobiła to nie będę musiał się
fatygować

25 cze 00:08
rumpek: 
Jakbyś miał jakieś jeszcze zadanka z reguły to bardzo chętnie je zrobię

Dzięki
25 cze 00:12
rumpek: Godzio sprawdzałeś może

?
25 cze 22:27
Godzio:
A już jest wieczór

? O 1 sprawdzę jakoś, bo zaraz wychodzę

(ewentualnie trochę później

)
25 cze 22:28
rumpek: No raczej jest

u mnie zbyt jasno nie jest xD
25 cze 22:31
Godzio:
Zad. 3 − do poprawy, reszta ok
25 cze 22:36
Godzio:
Popraw szybko to jeszcze zdążę sprawdzić

25 cze 22:36
Godzio: Zad. 8 Ile można otrzymać wyników, rzucając:
a) pięć razy monetą lub pięcioma monetami:
2 * 2 * 2 * 2 * 2 (każda moneta ma 2 wyniki − R lub O )
b) dwa razy kostką i trzy razy monetą?
6 * 6 * 2 * 2 * 2 (kostka ma 6 wyników, moneta 2 )
25 cze 22:39
Godzio: Zad. 9 Jest blok 8 piętrowy i 5 ludzi, na ile sposobów mogą wysiąść pasażerowie,
a) dowolnie:
Każdy pasażer może wysiąść na 8 sposobów: 8 * 8 * 8 * 8 * 8
b) każdy na innym piętrze
Pierwszy: 8
Drugi: 7
Trzeci:6 itd
8 * 7 * 6 * 5 * 4 = ...
Zad. 10 Jest 8 pudełek i 9 kul, na ile sposobów można umieścić kule w pudełkach
a) dowolnie
b) wszystkie znajdą się w różnych pudełkach
[a,b −− możesz zrobić sam]
c) wszystkie kule znajdą się w 3 pudełkach −− tutaj trzeba użyć kombinacji, podpowiem na
| | | | 8! | | 8! | | 5! * 6 * 7 * 8 | |
początek: | = |
| = |
| = |
| = 7 * 8 |
| | | (8 − 3)! * 3! | | 5! * 3! | | 5! * 6 | |
Teraz spróbuj z reguły mnożenia dojść do wyniku
7 * 8 * [ ? ? ? ]
25 cze 22:44
Godzio:
Fachowo to się nazywa:
Zad. 9
a) Wariacje z powtórzeniami ( n
k )
| | n! | |
b) Wariacje bez powtórzeń ( |
| |
| | (n − k)! | |
25 cze 22:45
rumpek: Jak do poprawy

mi tam tyle samo wychodzi 72

25 cze 22:46
Godzio:
A dobra, zobaczyłem że liczyłeś jeden przypadek, a nie zobaczyłem że pod spodem jest drugi

Jest git

25 cze 22:47
rumpek: 
25 cze 22:48
rumpek: Jakbyś miał jeszcze coś z reguły mnożenia to bardzo chętnie. A w następnym tygodniu
permutacje i kombinacje. A na koniec wariacje i rozróżnianie tego dziadostwa

25 cze 22:49
Godzio:
| | | |
To | − to wybór 3 pudełek z 8 |
| | |
25 cze 22:50
Godzio:
Ale 10 proszę mi tu zrobić

25 cze 22:50
rumpek: Zrobię

kiedyś

25 cze 22:53
Godzio:
Teraz, z reguły mnożenia

25 cze 22:53
rumpek:
Zad 10
a) 9 * 8 = 72
b) 9 * 8 = 72
72 − 8 = 64
25 cze 22:55
Godzio:
a) 8 pudełek, 9 kul, każda kula ma 8 możliwości wejścia do pudełek (bo dowolnie:
8 * 8 * 8 * 8 * 8 * 8 * 8 * 8 * 8 = 8
9
b) nie ma takiej możliwości, żeby wszystkie były w innych pudełkach

| | | |
c) Wybieram 3 pudełka z 8: | |
| | |
Każda kula ma 3 możliwości: 3 * 3 * 3 * 3 * 3 * 3 * 3 * 3 * 3 = 3
9
Odrzucam możliwość że wszystkie znajdą się w 1 pudełku lub drugim lub trzecim: − 3
(mają się znaleźć w 3 pudełkach, to żadne nie może być puste)
| | | |
Więc całkowita odpowiedź: | (39 − 3) = ... |
| | |
25 cze 23:01
rumpek:
A odnośnie 10 c)
| | | |
To ta kombinacja | to jest tylko wybranie pudełka, tak (8 * 7) ? |
| | |
25 cze 23:01
Godzio:
Tak
25 cze 23:02
Godzio:
Dobra ja wychodzę, narazie

25 cze 23:02
rumpek: Ok, dzięki

A że w tym 10 a) się rąbnąłem to aż szok

kilka postów wyżej robiłem prawie
taki sam podpunkt "z Tinki Winki

"
25 cze 23:04
 Trochę szybciej niż zapowiadałem
Kąty zaznaczaj na figurach przestrzennych które mają w podstawie trójkąt lub czworokąt
może być foremny [ to na czerwono chce żeby był trójkąt ]
Narysuj kąt:
a) W graniastosłupie:
− między ścianami bocznymi
− między przekątną ściany bocznej, a sąsiednią ścianą boczną
− między przekątnymi sąsiednich ścian bocznych
− między przekątną ściany bocznej, a płaszczyzną podstawy
b) W ostrosłupie:
− między ścianami bocznymi
− nachylenia ściany bocznej do płaszczyzny podstawy
− nachylenia krawędzi bocznej do płaszczyzny podstawy
Dodatkowo, gdzie leży spodek wysokości w ostrosłupie jeśli:
a) wszystkie krawędzie są równe lub padają pod tym samym kątem na płaszczyznę podstawy
b) wszystkie ściany boczne są nachylone do płaszczyzny podstawy pod tym samym kątem
Trochę szybciej niż zapowiadałem
Kąty zaznaczaj na figurach przestrzennych które mają w podstawie trójkąt lub czworokąt
może być foremny [ to na czerwono chce żeby był trójkąt ]
Narysuj kąt:
a) W graniastosłupie:
− między ścianami bocznymi
− między przekątną ściany bocznej, a sąsiednią ścianą boczną
− między przekątnymi sąsiednich ścian bocznych
− między przekątną ściany bocznej, a płaszczyzną podstawy
b) W ostrosłupie:
− między ścianami bocznymi
− nachylenia ściany bocznej do płaszczyzny podstawy
− nachylenia krawędzi bocznej do płaszczyzny podstawy
Dodatkowo, gdzie leży spodek wysokości w ostrosłupie jeśli:
a) wszystkie krawędzie są równe lub padają pod tym samym kątem na płaszczyznę podstawy
b) wszystkie ściany boczne są nachylone do płaszczyzny podstawy pod tym samym kątem
 a) Graniastosłup
− między ścianami bocznymi − przy nim w graniastosłupie mam najwięcej wątpliwości
Rysunek powyżej
a) Graniastosłup
− między ścianami bocznymi − przy nim w graniastosłupie mam najwięcej wątpliwości
Rysunek powyżej 




 To może wyjdźmy od czegoś czego wiem:
To w ostrosłupie − dwuścienny tak zwany − między ścianami bocznymi, tak
To może wyjdźmy od czegoś czego wiem:
To w ostrosłupie − dwuścienny tak zwany − między ścianami bocznymi, tak  ?
?

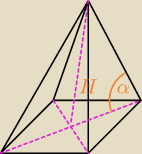 −nachylenia ściany bocznej do płaszczyzny podstawy :
Tak czy nie tak
−nachylenia ściany bocznej do płaszczyzny podstawy :
Tak czy nie tak  ?
?

 Właśnie mi się to myli przykład wyżej − narysowałem kąt między przekątną a podstawą w
sześcianie (chociaż łatwiej idzie napisać kąt między przekątną a przekątną podstawy )
Właśnie mi się to myli przykład wyżej − narysowałem kąt między przekątną a podstawą w
sześcianie (chociaż łatwiej idzie napisać kąt między przekątną a przekątną podstawy )
 Kąt między przekątną a ścianą boczną w sześcianie
Kąt między przekątną a ścianą boczną w sześcianie



 ?
?

 To jest taki kąt który zawsze się myli, a jest najprostszy
To jest taki kąt który zawsze się myli, a jest najprostszy 
 Jutro mam cały dzień na kąty
Jutro mam cały dzień na kąty  A po kątach do prostych rachunków
i na końcu rzeźnia
A po kątach do prostych rachunków
i na końcu rzeźnia 
 Takie pytanie: to wyżej to jest kąt między ścianami bocznymi w graniastosłupie, tak? Sorki, że
taki krzywy
Takie pytanie: to wyżej to jest kąt między ścianami bocznymi w graniastosłupie, tak? Sorki, że
taki krzywy 

 A to nie są kąty między ścianami bocznymi
A to nie są kąty między ścianami bocznymi  ?
?

 nawet się nie skapnąłem
nawet się nie skapnąłem

 między przekątną ściany bocznej a ściany bocznej i teraz pytanie czy to trochę podobne jest do
kąta między ścianami bocznymi ?
między przekątną ściany bocznej a ściany bocznej i teraz pytanie czy to trochę podobne jest do
kąta między ścianami bocznymi ? 
 między przekątną ściany bocznej a podstawą
między przekątną ściany bocznej a podstawą
 ?
?
 , tak?
, tak?
 Zaryzykuje − ten kąt to ten między sąsiednimi sianami bocznymi
Zaryzykuje − ten kąt to ten między sąsiednimi sianami bocznymi  ?
?
 to tak wygląda myślałem, że rysować jakieś takie
to tak wygląda myślałem, że rysować jakieś takie  a tu najprostsze jakie może być xD
a tu najprostsze jakie może być xD

 Trzeba dokończyć ostrosłupy
Trzeba dokończyć ostrosłupy 
 To ten co już rysowałem − między ścianami bocznymi tak zwany dwuścienny
To ten co już rysowałem − między ścianami bocznymi tak zwany dwuścienny 
 A taki może być "między ścianami bocznymi" o podstawie czworokątu?
A taki może być "między ścianami bocznymi" o podstawie czworokątu?

 To raczej nie jest ten kąt "między ścianami bocznymi"
Co do pytania, to chyba będzie taki kąt
To raczej nie jest ten kąt "między ścianami bocznymi"
Co do pytania, to chyba będzie taki kąt





 A jak w ostrosłupie narysować kąt między ścianą boczną a przekątną ściany bocznej. Tak o?
A jak w ostrosłupie narysować kąt między ścianą boczną a przekątną ściany bocznej. Tak o?

 i to była największa wątpliwość xD
i to była największa wątpliwość xD
 nachylenie krawędzi bocznej do płaszczyzny podstawy
nachylenie krawędzi bocznej do płaszczyzny podstawy

 kąt nachylenia ściany bocznej do płaszczyzny podstawy = coś takiego?
kąt nachylenia ściany bocznej do płaszczyzny podstawy = coś takiego?
 śmigam na rower, potem dokończę rysowanie tych wysokości bodajże
śmigam na rower, potem dokończę rysowanie tych wysokości bodajże  bo tylko one
zostały. Więcej kątów nie ma, które mogą pojawić się w zadaniach?
bo tylko one
zostały. Więcej kątów nie ma, które mogą pojawić się w zadaniach?

 ?
?

 ale jak wszystkie krawędzie są równe, to jest to czworościan foremny tak
ale jak wszystkie krawędzie są równe, to jest to czworościan foremny tak  ? I wysokość na
rysunku wyżejY
? I wysokość na
rysunku wyżejY


 )
)


 teraz powtórzyć wzory i za niedługo poproszę o jakieś proste zadania
teraz powtórzyć wzory i za niedługo poproszę o jakieś proste zadania  a po
prostych do rzeźniczych
a po
prostych do rzeźniczych 
 Godzio mam takie pytanie odnośnie takiego zadania:
trzeba udowodnić, że |BP| = |DR| a APQR i ABCD są kwadratami.
To skleiłem coś takiego:
na podstawie przystawania (bkb) trójkątów: ABP i ADR
1o Kwadrat ABCD ma wszystkie boki równe, więc podstawy trójkątów (ABP i ADR ) są równe:
|AB| = |AD|
2o Kwadrat APQR masz wszystkie boki równe, więc boki trójkątów (ABP i ADR) są równe:
|AP| = |AR|
3o Każdy kwadrat masz 4 kąty proste (4 * 90o = 360o). Przy każdym wierzchołku ma kąt 90o,
więc: w kwadracie ABCD mamy: ∡DAP = 90o − ∡BAP, natomiast w kwadracie APQR mamy:
∡DAR = 90o − ∡DAP ⇒ ∡DAR = 90o − (90o − ∡BAP) ⇒∡DAR = ∡BAP. Więc kąty są równe.
Na podstawie przystawania trójkątów wykazałem, iż odcinki |BP| i |DR| są równej długości.
c.n.u.
Godzio mam takie pytanie odnośnie takiego zadania:
trzeba udowodnić, że |BP| = |DR| a APQR i ABCD są kwadratami.
To skleiłem coś takiego:
na podstawie przystawania (bkb) trójkątów: ABP i ADR
1o Kwadrat ABCD ma wszystkie boki równe, więc podstawy trójkątów (ABP i ADR ) są równe:
|AB| = |AD|
2o Kwadrat APQR masz wszystkie boki równe, więc boki trójkątów (ABP i ADR) są równe:
|AP| = |AR|
3o Każdy kwadrat masz 4 kąty proste (4 * 90o = 360o). Przy każdym wierzchołku ma kąt 90o,
więc: w kwadracie ABCD mamy: ∡DAP = 90o − ∡BAP, natomiast w kwadracie APQR mamy:
∡DAR = 90o − ∡DAP ⇒ ∡DAR = 90o − (90o − ∡BAP) ⇒∡DAR = ∡BAP. Więc kąty są równe.
Na podstawie przystawania trójkątów wykazałem, iż odcinki |BP| i |DR| są równej długości.
c.n.u. 


 ?
?





 Przynajmniej mniej roboty i nie musisz nic rysować.
Przynajmniej mniej roboty i nie musisz nic rysować.


 do tego podpunktu mam najwięcej wątpliwości ale zaryzykuję:
Wszystkich możliwości jest 81. Są trzy torebki:
1o przypadek:
Gdy czerwona jest pusta, a w zielonej i niebieskiej jest co najmniej po jednym zdjęciu.
Wyliczyłem to wyżej jest takich możliwości 1.
2o przypadek:
Gdy zielona jest pusta, a w czerwonej i niebieskiej jest co najmniej po jednym zdjęciu. Też
jest 14 (na podstawie przypadku pierwszego)
3o przypadek:
Gdy niebieska jest pusta, a w czerwonej i zielonej jest co najmniej po jednym zdjęciu. Również
jest 14 (dwa przypadki wyżej)
Więc raczej:
81 − 14 * 3 = 81 − 42 = 39
Jednak jeszcze chyba trzeba sprawdzić kiedy wszystkie zdjęcia znajdują się w jednej torebce −
są trzy torebki więc są trzy możliwości.
Więc dodatkowo:
39 − 3 = 36
Z tym miałem najwięcej wątpliwości, proszę sprawdzić
do tego podpunktu mam najwięcej wątpliwości ale zaryzykuję:
Wszystkich możliwości jest 81. Są trzy torebki:
1o przypadek:
Gdy czerwona jest pusta, a w zielonej i niebieskiej jest co najmniej po jednym zdjęciu.
Wyliczyłem to wyżej jest takich możliwości 1.
2o przypadek:
Gdy zielona jest pusta, a w czerwonej i niebieskiej jest co najmniej po jednym zdjęciu. Też
jest 14 (na podstawie przypadku pierwszego)
3o przypadek:
Gdy niebieska jest pusta, a w czerwonej i zielonej jest co najmniej po jednym zdjęciu. Również
jest 14 (dwa przypadki wyżej)
Więc raczej:
81 − 14 * 3 = 81 − 42 = 39
Jednak jeszcze chyba trzeba sprawdzić kiedy wszystkie zdjęcia znajdują się w jednej torebce −
są trzy torebki więc są trzy możliwości.
Więc dodatkowo:
39 − 3 = 36
Z tym miałem najwięcej wątpliwości, proszę sprawdzić  I proszę o jeszcze jakieś zadania, ale w osobnym temacie, aby nie ciągnąć tego ze stereometrii
tak
I proszę o jeszcze jakieś zadania, ale w osobnym temacie, aby nie ciągnąć tego ze stereometrii
tak  thx
thx
 Bo na razie temu chcę czas poświęcić
Bo na razie temu chcę czas poświęcić  Godzio
jakbyś miał już czas to jakimiś zadaniami nie pogardziłbym
Godzio
jakbyś miał już czas to jakimiś zadaniami nie pogardziłbym 


 Parzyste: {0,2,4}
Nieparzyste: {1,3,5}
Sorki xD nieuwaga
Parzyste: {0,2,4}
Nieparzyste: {1,3,5}
Sorki xD nieuwaga 
 ?
?

 )
b) (to to w ogóle permutacją zalatuje
)
b) (to to w ogóle permutacją zalatuje  − muszę o niej doczytać)
Jak to zrobić regułą mnożenia?
Zad 3
D1 C1 D2 C2 D3 C3
Dziewczyny = 3!
Chłopcy = 3!
6 * 6 = 36
C1 D1 C2 D2 C3 D3
Dziewczyny = 3!
Chłopcy = 3!
6 * 6 = 36
Sumując:
36 + 36 = 72
Zad 4
Ze zbioru {0,1,2,3,4}
− − − − −
1 2 3 4 5
Pierwsze miejsce mogę obsadzić na 4 sposoby (bez 0)
Drugie miejsce mogę obsadzić na 4 sposoby (bez pierwszej liczby)
Trzecie miejsce mogę wybrać na 3 sposoby (bez dwóch poprzednich)
Czwarte miejsce mogę wybrać na 2 sposoby (bez trzech poprzednich)
Ostatnie tylko na jeden sposób
4 * 4 * 3 * 2 * 1 = 96
Zad 5
Liczby to: {0,1,2,3,4,5,6,7,8,9} jest ich 10 więc:
− − − −
1 2 3 4
Pierwszą liczbę mogę wybrać na 9 sposobów
Drugą liczbę mogę wybrać na 9 sposobów
Trzecią liczbę mogę wybrać na 8 sposób
Czwartą liczbę mogę wybrać na 7 sposobów
Więc:
9 * 9 * 8 * 7 = 4536
Zad 6
Ze zbioru {0,1,2,3,4,5,6,7,8,9}
Nieparzysta liczba − na końcu liczby nie parzyste więc: {1,3,5,7,9} − jest ich 5
Więc:
− − −
1 2 3
Ostatnią liczbę mogę wybrać na 5 sposobów.
Pierwszą liczbę mogę wybrać na 8 sposobów
Drugą liczbę mogę wybrać na 8 sposobów
8 * 8 * 5 = 320
Zad 7
a)
Ze zbioru {0,1,2,3,4,5,6,7,8,9} wybieram parzyste i mam:
{0,2,4,6,8} − 8 możliwości
− − −
1 2 3
Ma być trzycyfrowa liczba więc mogę ją wybrać na: (mogą się powtarzać)
4 * 5 * 5 = 100
b)
− − −
1 2 3
Pierwszą mogę wybrać tylko {5,6} czyli na dwa sposoby
Druga mogę wybrać na 10 sposobów
Trzecią na też na 10 sposobów.
2 * 10 * 10 = 200 (odejmuję jedną bo może być ułożenie 500
− muszę o niej doczytać)
Jak to zrobić regułą mnożenia?
Zad 3
D1 C1 D2 C2 D3 C3
Dziewczyny = 3!
Chłopcy = 3!
6 * 6 = 36
C1 D1 C2 D2 C3 D3
Dziewczyny = 3!
Chłopcy = 3!
6 * 6 = 36
Sumując:
36 + 36 = 72
Zad 4
Ze zbioru {0,1,2,3,4}
− − − − −
1 2 3 4 5
Pierwsze miejsce mogę obsadzić na 4 sposoby (bez 0)
Drugie miejsce mogę obsadzić na 4 sposoby (bez pierwszej liczby)
Trzecie miejsce mogę wybrać na 3 sposoby (bez dwóch poprzednich)
Czwarte miejsce mogę wybrać na 2 sposoby (bez trzech poprzednich)
Ostatnie tylko na jeden sposób
4 * 4 * 3 * 2 * 1 = 96
Zad 5
Liczby to: {0,1,2,3,4,5,6,7,8,9} jest ich 10 więc:
− − − −
1 2 3 4
Pierwszą liczbę mogę wybrać na 9 sposobów
Drugą liczbę mogę wybrać na 9 sposobów
Trzecią liczbę mogę wybrać na 8 sposób
Czwartą liczbę mogę wybrać na 7 sposobów
Więc:
9 * 9 * 8 * 7 = 4536
Zad 6
Ze zbioru {0,1,2,3,4,5,6,7,8,9}
Nieparzysta liczba − na końcu liczby nie parzyste więc: {1,3,5,7,9} − jest ich 5
Więc:
− − −
1 2 3
Ostatnią liczbę mogę wybrać na 5 sposobów.
Pierwszą liczbę mogę wybrać na 8 sposobów
Drugą liczbę mogę wybrać na 8 sposobów
8 * 8 * 5 = 320
Zad 7
a)
Ze zbioru {0,1,2,3,4,5,6,7,8,9} wybieram parzyste i mam:
{0,2,4,6,8} − 8 możliwości
− − −
1 2 3
Ma być trzycyfrowa liczba więc mogę ją wybrać na: (mogą się powtarzać)
4 * 5 * 5 = 100
b)
− − −
1 2 3
Pierwszą mogę wybrać tylko {5,6} czyli na dwa sposoby
Druga mogę wybrać na 10 sposobów
Trzecią na też na 10 sposobów.
2 * 10 * 10 = 200 (odejmuję jedną bo może być ułożenie 500  )
200 − 1 = 199 i mamy odpowiedź
)
200 − 1 = 199 i mamy odpowiedź  Zad 8 9 i 10
to na pewno da się zrobić regułą mnożenia? bo tylko o takie na razie zadanka prosiłem
Zad 8 9 i 10
to na pewno da się zrobić regułą mnożenia? bo tylko o takie na razie zadanka prosiłem 

 zapomniałem, że Krysia i Iza też mogą się zamienić stronami
zapomniałem, że Krysia i Iza też mogą się zamienić stronami  2! − wiem skąd
3! − wiem skąd
4 − nie do końca wiem (czyżby z tego, że są cztery przypadki?)
2! − wiem skąd
3! − wiem skąd
4 − nie do końca wiem (czyżby z tego, że są cztery przypadki?)  Dziękuje
Dziękuje  (reszta dobrze?)
(reszta dobrze?)
 Zadania sprawdzę jutro wieczorem, chyba że Eta to już zrobiła to nie będę musiał się
fatygować
Zadania sprawdzę jutro wieczorem, chyba że Eta to już zrobiła to nie będę musiał się
fatygować 
 Jakbyś miał jakieś jeszcze zadanka z reguły to bardzo chętnie je zrobię
Jakbyś miał jakieś jeszcze zadanka z reguły to bardzo chętnie je zrobię  Dzięki
Dzięki
 ?
?
 ? O 1 sprawdzę jakoś, bo zaraz wychodzę
? O 1 sprawdzę jakoś, bo zaraz wychodzę  (ewentualnie trochę później
(ewentualnie trochę później  )
)
 u mnie zbyt jasno nie jest xD
u mnie zbyt jasno nie jest xD

 mi tam tyle samo wychodzi 72
mi tam tyle samo wychodzi 72 
 Jest git
Jest git 



 kiedyś
kiedyś 



 A że w tym 10 a) się rąbnąłem to aż szok
A że w tym 10 a) się rąbnąłem to aż szok  kilka postów wyżej robiłem prawie
taki sam podpunkt "z Tinki Winki
kilka postów wyżej robiłem prawie
taki sam podpunkt "z Tinki Winki "
"