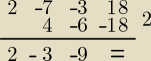D18 = {−1,1,−2,2,−3,3,−6,6,−9,9,−18,18}
W(x) = 2x3 − 7x2 − 3x + 18
W(−1) = −2 − 7 + 3 + 18 ≠ 0
W(1) = 2 − 7 − 3 + 18 ≠ 0
W(−2) = −16 − 28 + 6 + 18 ≠ 0
W(2) = 16 − 28 − 6 + 18 = 0
Skoro dzieli się to jedziemy (zrobię to Heronem − tabelka wyżej)
Otrzymujemy:
(2x2 − 3x − 9)(x − 2) = 0
Δ = 9 + 72 = 81 ⇒ √Δ = 9
| 3 − 9 | 6 | 3 | ||||
x1 = | = − | = − | ||||
| 4 | 4 | 2 |
| 3 + 9 | 12 | |||
x2 = | = | = 3 | ||
| 4 | 4 |
| 3 | ||
2(x + | )(x − 3)(x − 2) = 0 | |
| 2 |
