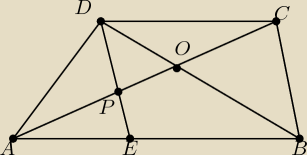
 Punkt E leży na podstawie trapezu ABCD w ten sposób, że AE = BE. Odcinki CA i CE przecinają
przekątną BD odpowiednio w punktach O i P. Udowodnij, że jeżeli DP = BO, to AD2 = BC2 +AD*BC
Jakoś nie mogę tego zadania ruszyć. Mam to wykazać przy użyciu trójkątów podobnych czy tw.
Talesa. Chodzi o proporcjonalność odcinków. Niestety nic sensownego nie otrzymałem. Czy mógłby
ktoś podać jakieś wskazówki (jeżeli ktoś to rozwiąże, proszę aby nie podawał rozwiązania, ale
jakąś wskazówkę, uwagę, która mnie naprowadzi na właściwy tor).
Będę bardzo wdzięczny.
Pozdrawiam.
Punkt E leży na podstawie trapezu ABCD w ten sposób, że AE = BE. Odcinki CA i CE przecinają
przekątną BD odpowiednio w punktach O i P. Udowodnij, że jeżeli DP = BO, to AD2 = BC2 +AD*BC
Jakoś nie mogę tego zadania ruszyć. Mam to wykazać przy użyciu trójkątów podobnych czy tw.
Talesa. Chodzi o proporcjonalność odcinków. Niestety nic sensownego nie otrzymałem. Czy mógłby
ktoś podać jakieś wskazówki (jeżeli ktoś to rozwiąże, proszę aby nie podawał rozwiązania, ale
jakąś wskazówkę, uwagę, która mnie naprowadzi na właściwy tor).
Będę bardzo wdzięczny.
Pozdrawiam.
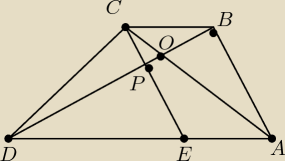 Przeprasza trochę namieszałem rysunek jest dla innych oznaczeń niż w poleceniu. (zwykle w ten
sposób jak w pierwszym poście oznaczam wierzchołki czworokąta, a to powinno być tak jak w tym
poście).
Za niedogodności przepraszam.
PS: Mam nadzieje, że nikt nie zaczął rozwiązywać przed wysłaniem mojego drugiego postu
Przeprasza trochę namieszałem rysunek jest dla innych oznaczeń niż w poleceniu. (zwykle w ten
sposób jak w pierwszym poście oznaczam wierzchołki czworokąta, a to powinno być tak jak w tym
poście).
Za niedogodności przepraszam.
PS: Mam nadzieje, że nikt nie zaczął rozwiązywać przed wysłaniem mojego drugiego postu 
| BO | CO | OP | |||
= | = | ||||
| DP | IA | BO |
| BO | OP | |||
Czyli | = | |||
| DP | BO |
| 1 | ||
Jeżeli BO = OP = DP i OP + DP + BO = BD, to DP = | BD | |
| 3 |
| DP | DB | |||
= | ||||
| DE | AD |
| 2 | 1 | |||
stąd otrzymuję, że DE = | AD czyli EA = BC = { | AD, a to nie spełnia tezy. | ||
| 3 | 3 |
| 1 | 2 | |||
Sorry DE = | AD, a BC = | AD | ||
| 3 | 3 |
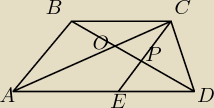
| |BO| | |DP| | |ED| | ||||
Zauważmy, że |BO| = |PD| ⇒ | = | = p, zauważmy teraz, że | ||||
| |OD| | |BP| | |PD| |
| |BC| | ||
= | ⇔ |ED| = |BC|*p czyli: | |
| |BP| |
| |BC| | |BC| | |BC|2 | |||
= |AD| = |BC| + |BC|*p / * | ⇒ |AD|2 = | + |BC|2 = | |||
| p | p | p |