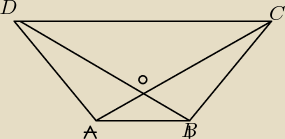
trapezy Miśka: Czworokąt ABCD jest trapezem. Udowodnij, że trójkaty AOD i CBO maja równe pole.

asd: ale to musi być równoramienny trapez nie pisze nic o tym ?

Miśka: nie nie ma takiej informacji...

hwdtel i x3: PΔ_ADO=0,5|OD||AO|(sin∡O) : PΔ_COB=0,5|OC||OB|sin(∡O)

	|AO|		|OB|		|CO|		|DO|
ΔAOB∼ΔCOD ;		=		;		=
	sinβ		sinα		sinβ		sinα

|AO||DO|		|OB||OC|
	=
sinαsinβ		sinαsinβ

PΔ_ADO = PΔ_COB cbdw

Bogdan: Najpierw trzeba pokazać, że odcinki e, f są równe.

	a		w + v		aw
Z podobieństwa trójkątów: ABD i EOD:		=		⇒ e =		.
	e		w		w + v

	a		w + v		aw
Z podobieństwa trójkątów: ABC i FOC:		=		⇒ f =		.
	f		w		w + v

Stąd e = f. Pola trójkątów AOE i BOF są równe, bo mają równe podstawy (e = f) i równe wysokości v. Pola trójkątów EOD i FOC są równe, bo mają równe podstawy (e = f) i równe wysokości w. Wobec tego P_AOD = P_BOC, co należało udowodnić.

Vax: Można to udowodnić w jeszcze prostszy sposób, zauważmy, że P_ABD = P_ABC, teraz oznaczmy P_ABO = P₁ , P_AOD = P₂ , P_BOC = P₃, naszą równość można zapisać: P₁+P₂ = P₁+P₃ /−P₁ P₂ = P₃ cnd Pozdrawiam.