planimetria (figury podobne)
TPB: Dany jest równoległobok ABCD, na krótszej przekątnej (BD) obrano punkt K. Poprowadzono przez
niego prostą, która przecina proste BC i CD w punktach odpowiednio L i M. Udowodnij, że AK
2 =
LK * LM
No i właśnie zacząłem robić ten przykład. Postanowiłem przekształcić tezę do takiej oto
postaci:
| AK | | LM | |
| = |
| . Mam tutaj stosunki pewnych boków. A zadanie jest z działu o trójkątach |
| LK | | AK | |
podobnych. Nie jestem w stanie tego udowodnić.
Jak na razie poprowadziłem przez punkt K prostą równoległą do boków BC i AD, która przecina
boki AB i CD w punktach P,Q. Otrzymałem 4 trójkąty podobne( w sumie 5, ale 1 jest raczej
nieprzydatny − MDA), ale za nic nie mogę udowodnić. Jestem ślepy geometrycznie

Proszę o jakieś wskazówki.
9 cze 10:34
krystek: Ale coś mi się nie zgadza ,(zamotało mnie?) poprowadzono prostą czy proste przez p. K?
9 cze 11:07
TPB: Wybacz masz rację, (pisałem z pamięci i zapomniałem o oczywistym fakcie) prosta przechodzące
przez punkt K przechodzi przez wierzchołek A, wtedy jest już wszystko ok.
Czyli prosta AK przecina proste BC oraz CD
9 cze 11:10
TPB:
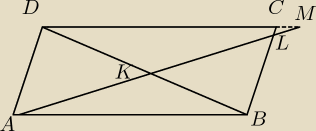
9 cze 11:13
krystek: I też mam jedno zadanie ,które ktoś chyba podał niedokładnie.
W trapezie ramiona do krótszej podstawy są pod kątem 135 i 60. dłuższa ramię ma 18cm .Oblicz
pole tego trapezu. wydawało mi się proste ,ale czegoś nie zauważam ,lub coś jest pominięte
,ponieważ nie mogę obliczyć podstaw.
9 cze 11:19
TPB: Spróbuję, ostatnio wiele zadań z geometrii przerabiam, zwłaszcza z planimetrii, to moja pięta
achillesowa. Ale staram się polubić geometrię, bo w niej najlepiej mogę sprawdzić logiczne
myślenia. Zawsze trzeba coś nowego zauważyć, a nie tak jak w równaniach gdzie wiele przykładów
leci się schematem. Zaraz sprawdzę Twoje zadanko.
9 cze 11:22
TPB: Cóż nie wiem, też nie mogę podstaw obliczyć. Wysokości, ramiona, fragmenty podstaw idą łatwo,
ale pozostaje mi pewien odcinek o tej samej długości zarówno na jednej jak i drugiej
podstawie, którego nie potrafię wyliczyć.
9 cze 11:32
Godzio:
Trzeba jeszcze pomóc co do zadania TPB ?
9 cze 11:33
krystek: I właśnie w tym jest problem ,Podejrzewam ,że ktoś niedokładnie podał zadanie.
Pozdrawiam.
9 cze 11:34
TPB: Już nie, kilka sekund temu udało mi się zrobić. Teraz męcze inne zadanie z równoległobokiem

9 cze 11:34
krystek: Witaj Godzio,spójrz na zadanie z trapezem, które w poprzednim moim poście umieszczone jest.
9 cze 11:36
Godzio:
Ok, już patrzę
9 cze 11:38
Godzio:
Masz do tego odpowiedź ?
Wyszło mi: P = 108(3 +
√3)
Ale jeszcze muszę posprawdzać

9 cze 11:48
Godzio:
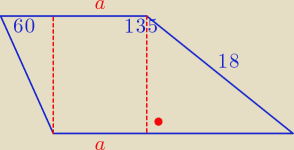
Jednak miałem błąd w rozumowaniu, chyba jednak zostało coś pominięte w tym zadaniu bo "a"
może mnie dowolną długość i niczym nie jest to ograniczone
9 cze 11:53
krystek: Dzięki ,upewniłes mnie w przypuszczeniach. Ktoś podał niedokładnie.
Miłego dnia życzę.
9 cze 12:03
Vax:
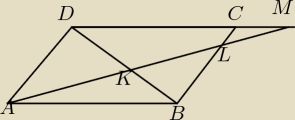
Co do 1 zadania, to teza jest błędna, prawidłowa jest równość |AK|
2 = |KL|*|KM|, zauważmy, że
| | KL | | AK | | AK * KB | |
ΔBKL ~ ΔAKD czyli |
| = |
| ⇒ KL = |
| , dodatkowo ΔABK ~ ΔDMK co daje |
| | KB | | KD | | KD | |
| | KM | | AK | | AK * DK | | AK*KB | | AK*DK | |
nam |
| = |
| ⇒ KM = |
| czyli KL * KM = |
| * |
| = |
| | DK | | BK | | BK | | KD | | BK | |
AK
2 cnd.
17 sie 15:06
 Proszę o jakieś wskazówki.
Proszę o jakieś wskazówki.



 Jednak miałem błąd w rozumowaniu, chyba jednak zostało coś pominięte w tym zadaniu bo "a"
może mnie dowolną długość i niczym nie jest to ograniczone
Jednak miałem błąd w rozumowaniu, chyba jednak zostało coś pominięte w tym zadaniu bo "a"
może mnie dowolną długość i niczym nie jest to ograniczone
 Co do 1 zadania, to teza jest błędna, prawidłowa jest równość |AK|2 = |KL|*|KM|, zauważmy, że
Co do 1 zadania, to teza jest błędna, prawidłowa jest równość |AK|2 = |KL|*|KM|, zauważmy, że