Określanie Dziedziny Funkcji
Daniel: Witam, mam mały problem ponieważ jutro zdaje matme a nie rozumiem kilku rzeczy a więc
| | x + 3 | |
y= |
| Nie wiem co zrobić z tą potęgą |
| | x2 + 9 | |
Pomóżcie z góry Dziękuję
9 cze 00:15
Bogdan:
Nic nie trzeba robić z tą potęgą.
Dziedziną jest R.
Dla dowolnej liczby rzeczywistej x suma x2 + 9 jest zawsze dodatnia, a więc w tym
przypadku mianownik jest zawsze większy od zera, a tym samym różny od zera.
9 cze 00:20
Daniel: Teraz rozumiem Dziękuję wrazie czego to bede jeszcze pisał bo mam cały dział Funkcji zaliczyc a
nie zabardzo to rozumiem
9 cze 00:21
Daniel: No i mam problem z wyznaczaniem miejsca zerowego funkcji
Wyznacz miejsca zerowe funkcji(o ile istnieja)
| | 2 | |
przykład 1 : y= |
| x − 2 , x∊ R |
| | 3 | |
| | 2 | |
przykład 2 : y= |
| x − 2 , x∊ (3,+∞) |
| | 3 | |
Bez ułamków no potrafie a z ułamkami nie mam pojecia jak sie za to zabrać
9 cze 00:59
ZKS:
A czego dokładnie nie rozumiesz?
9 cze 01:13
Daniel: Ogółem próbowałem zrobić to z 5 razy i cały czas jakies kosmiczne liczy mi wychodza na necie
znalazłem tylko bez ułamków a z tym nie moge sie połapać
9 cze 01:22
ZKS:
A jak byś z tego wyliczył miejsce zerowe y = ax + b ?
9 cze 01:25
Daniel: Tzn? do mnie musisz jak do dziecka bo mam kose z matmy i właśnie jutro bede próbował zdać
9 cze 01:26
Daniel: Mam prośbe daj może Swój nr GG i by było szybciej
9 cze 01:29
ZKS:
Już jestem
Wzór funkcji liniowej wygląda tak y = ax + b a jak będzie wyglądało miejsce zerowe jak się je
oblicza?
9 cze 01:36
Daniel: No ja próbowałem w ten sposób
Zły wynik wychodził jakiś kosmiczny
9 cze 01:42
ZKS:
| | 2 | | 2 | |
Zobacz czy 2 = |
| x nie jest równe |
| x = 2 ? Bo u Ciebie jak przenosisz to Ci się |
| | 3 | | 3 | |
| | 2 | |
zmienia znak przy 2 ale przy |
| x już nie |
| | 3 | |
9 cze 01:47
9 cze 01:48
Daniel: no x=3
9 cze 01:51
ZKS:
Dokładnie
Teraz spróbuj zrobić następny zapisując swoje obliczenia.
9 cze 01:53
Daniel: A jeśli chodzi o wyznaczanie dziedziny bo też mi nie idzie
Przykład: y=
√2 − |x+4|
w ODP; jest Że ma wyjść<−6,−2>
I też nie wiem skąd to sie bierze
9 cze 01:56
ZKS:
Jaka jest dziedzina funkcji takiego czegoś y = √x ?
9 cze 01:58
Daniel: no x∊R i liczba podpierwiastkowa nie może być ujemna
np: √x + 2 rozumiem bo to wyjdzie Df=R/{−2}
9 cze 02:03
ZKS:
√x + 2 Df nie jest R \ {−2}
Liczba pod pierwiastkiem nie może być ujemna jak sam powiedziałeś czyli
y = √x dziedziną tego co będzie?
9 cze 02:06
Daniel: NO D=<0,+∞)
9 cze 02:08
ZKS:
Właśnie a więc dziedziną √x + 2 co będzie ?
9 cze 02:11
Daniel: Df=<−2.∞)?
9 cze 02:14
ZKS:
Zgadza się to jaką będziesz miał dziedzinę dla √2 − |x + 4|
9 cze 02:17
ZKS:
Jak coś zapisz obliczenia to zobaczymy gdzie robisz błąd jak coś.
9 cze 02:21
Daniel: No będzie <−6,−2> alt to ja wiem z ODP rozumiem czemu −6 ale nie wiem czemu akurat −2 jak by
było −3 to by nie było ujemne
9 cze 02:22
ZKS:
Zapisz wszystko od początku do końca jak robisz to wszystko wtedy na pewno zrozumiesz.
9 cze 02:26
Daniel:
2−x+4
2−x+4≥0
−x≥−6//:(−1)
x≥6
9 cze 02:31
ZKS:
Mamy tak 2 − |x + 4| ≥ 0 a nie 2 − x + 4 ≥ 0 popraw i zapisz obliczenia.
9 cze 02:33
Daniel:
−2x−8≥0
−2x = 8//:(−2)
x =−4 i źłe
9 cze 02:38
ZKS:
Źle przenieś tą 2 na drugą stronę i oczywiście znowu zapisz co dalej robisz.
9 cze 02:44
Daniel: na kilka razy próbowałem
−|x+4|≥−2//:(−1)
x−4≥2
x≥6
−x−4≥−2
−x≥2//:(−1)
x≥−2
9 cze 02:51
ZKS:
Jeżeli mnożymy przez (−1) to co się dzieje ze znakiem nierówności?
9 cze 02:53
Daniel: no odwraca sie
9 cze 02:54
Daniel: ale to chyba nie zmienia wyniku
9 cze 02:55
ZKS:
Tak i dlatego będziesz miał
−|x + 4| ≥ −2 / * (−)
|x + 4| ≤ 2 Teraz dokończ i oczywiście pokaż swoje obliczenia.
9 cze 02:56
Daniel:
x≤2−4
x≤−2
nie wiem juz sie całkowicie pogubiłem
9 cze 02:59
ZKS:
|x + 4| − to jest wartość bezwzględna (moduł) a więc rozważasz dwa przypadki rozumiesz?
9 cze 03:00
Daniel: Ledwo co
9 cze 03:03
ZKS:
|x + 2| = 1 Potrafiłbyś to rozwiązać czy nie za bardzo?
9 cze 03:07
Daniel: no to tak x=−3
9 cze 03:12
ZKS:
Rozważasz dwa przypadki czyli :
x + 2 = 1 lub x + 2 = −1
x = −1 lub x = −3
Zrób teraz to |x + 10| = 4
9 cze 03:17
Daniel: x+10=−4
x=−4−10
x=−14
LUB
x+10=4
x=4−10
x=−6
9 cze 03:22
ZKS:
Dobrze. To teraz zrób nierówność z modułem
|x − 6| > 3 , |x + 2| ≥ 4 , |x − 12| < 10 , |x − 1| ≤ 2
9 cze 03:25
ZKS: Zrób po kolei i zapisuj wszystko co i jak.
9 cze 03:26
ZKS:
|x + a| > b ⇒ x + a > b lub x + a < −b
|x + a| < b ⇒ x + a < b i x + a > −b
9 cze 03:31
Daniel: x−6>3
x>3−6
x>−3
9 cze 03:33
Daniel: o to chodzi ?
9 cze 03:36
ZKS:
Brakuje drugiej części
|x − 6| > 3 ⇒ x − 6 > 3 lub x − 6 < −3
x > 3 + 6 lub x < −3 + 6
Dokończ i zapisz sumę przedziałów.
9 cze 03:38
Daniel: x>9 Lub x<3
9 cze 03:43
ZKS:
Zapisz to jako sumę przedziałów
x < 3 lub x > 9 ⇒ x∊
9 cze 03:45
Daniel: No właśnie nie czaje jak
9 cze 03:47
ZKS:
Spełniają to liczby mniejsze od 3 lub liczby większe od 9
x∊(−∞,3) ∪ (9,∞)
Teraz zrób kolejne uwzględniając wszystko co Ci napisałem.
9 cze 03:51
Daniel: |x+2|≥4 ⇒ x+2>4 Lub x+2<−4
x>4−2 Lub x<−4−2
x>2 Lub x<−6
x∊(−∞,−6> ∪ <2 , ∞)
9 cze 03:56
Daniel: DObrze?
9 cze 03:56
ZKS:
Git. Tylko że muszę się przyczepić do tego że masz
|x + 2| ≥ 4 ⇒ x + 2 > 4 lub x + 2 < −4
a powinno być x + 2 ≥ 4 lub x + 2 ≤ −4
Suma przedziałów poprawnie zapisana ale pamiętaj o tym co napisałem.
To teraz kolejne spróbuj.
9 cze 04:03
Daniel: |x−12|<10⇒x−12<10 Lub x−12 >−10
x<22 Lub x> 2
x∊(−∞,22>∪<2,∞)
Troszke poleciałem na skróty ale wynik wydaje mi sie dobry
9 cze 04:08
ZKS:
|x − 12| < 10 ⇒ x − 12 < 10 i x − 12 > −10
Zobacz jak zapisałeś przedział
x∊(−∞,22> ∪ <2,∞) 22 jest większe przecież od 2.
Tutaj nie bierzesz sumę przedziałów tylko ich iloczyn. Popraw. A i jeszcze to jest nie równość
zwykła a nie ostra że zamykasz przedział czyli nie > tylko ).
9 cze 04:15
ZKS:
Zrobię ja ten a następny będzie dla Ciebie.
9 cze 04:16
ZKS:
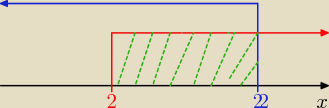
|x − 12| < 10 ⇒ x − 12 < 10 i x − 12 > −10
x < 22 i x > 2 Iloczynem tych dwóch przedziałów jest x∊(2,22)
9 cze 04:19
ZKS:
Teraz zrób następny.
9 cze 04:20
Daniel: x∊(−∞2)∪(22,∞)
9 cze 04:21
Daniel: z tym obrazkiem?
9 cze 04:22
ZKS:
Bez bez chciałem Ci tylko to zilustrować jak wygląda taki właśnie przedział.
9 cze 04:24
ZKS:
Czyli końcowy wynik tamtego to x∊(2,22) mam nadzieje że to rozumiesz.
9 cze 04:25
Daniel: tak rozzumiem musiałem szybko z psem wyjsc
9 cze 04:32
ZKS:
O tej porze z psem chyba że bardzo chciał iść na ten dwór
9 cze 04:33
Daniel: |x−1|≤2 ⇒ x−1≤2 i x−1≥−2
x≤3 x≥−3
x∊(−∞.−3)∪(3,∞) x∊(−3,3)
9 cze 04:36
Daniel: No obudził sie a był o 22 a to szczeniak
9 cze 04:37
Daniel: I jak
9 cze 04:38
ZKS:
Rozwiązuj powoli bo już widzę błędy niestety popraw. O szczeniak a jaka rasa?
9 cze 04:43
Daniel: Cocker Spaniel
9 cze 04:45
Daniel: Nie wiem gdzie jest błąd
9 cze 04:46
ZKS:
x ≤ 3 − dobrze ale x ≥ 3 jest źle bo x − 1 ≥ −2 ⇒ x ≥ −1
Podaj iloczyn przedziałów.
9 cze 04:49
ZKS:
To fajny piesek jak tak.
9 cze 04:50
Daniel: a Tutaj no racja i to jest wszystko do obliczenia Dziedziny?
9 cze 04:50
Daniel: x∊(−1,3)
9 cze 04:51
ZKS:
Już myślałem że jest dobrze. To jest nierówność ostra czyli jak będzie wyglądał przedział?
9 cze 04:53
Daniel: x∊<−1,3>
9 cze 04:55
ZKS:
Teraz się zgadzam z Twoją odpowiedzią. Rozwiąż jeszcze te |1 − x| > 2 |8 − x| ≤ 4
9 cze 04:56
ZKS:
I za chwilkę zajmiemy się Twoją dziedziną.
9 cze 04:57
Daniel: |1 − x| > 2 ⇒1−x>2 i 1−x<−2
−x>1 −x<−3
x<−1 x>3
x∊(−
∞,−1)∪(3,
∞) z∊<−1,3)
Napewno coś namieszałem
9 cze 05:02
ZKS:
Właśnie nie namieszałeś tylko wszystko poprawnie zrobiłeś. Nigdy się nie śpiesz bo wtedy zawsze
popełnia się głupie błędy.
I który przedział dajesz ostatecznie ten x∊(−∞,−1) ∪ (3,∞) czy x∊(−1,3)
9 cze 05:05
Daniel: ten 1
9 cze 05:06
ZKS:
To dobrze
Pamiętaj jak jest |x + a| > b to wtedy mamy sumę zbiorów a jeżeli |x + a| < b iloczyn
9 cze 05:09
ZKS:
To teraz Twoja dziedzina.
2 − |x + 4| ≥ 0
9 cze 05:10
ZKS:
Spokojnie zrób żeby było wszystko poprawnie.
9 cze 05:10
Daniel: ok
to co przechodzimy do dziedziny?
9 cze 05:10
ZKS:
Tak bo widzę że już opanowałeś moduł.
Zrób tą dziedzinę 2 − |x + 4| ≥ 0
9 cze 05:14
Daniel: |x+4|≥−2⇒x+4≥−2 i x+4≤2
x≥−6 x≤−2
(−∞,−6)∪(−2,∞)
9 cze 05:15
ZKS:
A dlaczego nie zmieniłeś znaku jak pomnożyłeś przez − ? Popraw.
9 cze 05:17
Daniel: Ja ogółem w 1 LO jestem
9 cze 05:17
Daniel: Ale ja nic nie mnożyłem napisze wszystko po kolei
9 cze 05:18
ZKS:
To sporo czasu jeszcze masz na przygotowanie do matury. A na jakim profilu jesteś?
9 cze 05:18
ZKS:
Napisz po kolei jeszcze raz.
9 cze 05:20
Daniel: |x+4|≥−2 ⇒ x+4≥−2 i x+4≤2
x≥−2−4 x≤2−4
x≥−6 x≤−2
(−∞,−6)∪(−2,∞)
9 cze 05:20
Daniel: Wojskowym
i mam Matme FIzyke i Angielski rozszerzony
9 cze 05:21
ZKS:
Źle.
2 − |x + 4| ≥ 0
−|x + 4| ≥ −2 / * −
|x + 4| ≤ 2 Dokończ.
9 cze 05:22
ZKS:
Może jeszcze matematyka Ci się spodoba i będziesz zdawał na rozszerzeniu
9 cze 05:22
Daniel: Aaa tutaj błąd rozpedziłem sie
9 cze 05:23
Daniel: no tylko musiałbym zaczać sie z niej uczyc
a nie potem siedziec po nocach ogółem bardzo
ci dziękuję że chciałeś mi pomoc
9 cze 05:24
ZKS:
To teraz jest najlepszy moment żeby opanować w bardzo dobrym stopniu matematykę podstawę jaki
rozszerzenie.
9 cze 05:26
Daniel: |x+4|≤2 ⇒ x+4≤2 i x+4≥−2
x≤−2 x≥−6
(−∞,−6)∪(−2,∞)
9 cze 05:26
ZKS:
A proszę bardzo i tak sobie mecz oglądam w między czasie
9 cze 05:26
Daniel: Skąd jesteś ogółem?
9 cze 05:27
Daniel: ja na 8 do szkoły lece i to napisze wróce o 16 to tu napisze jak poszło
9 cze 05:27
ZKS:
To jest iloczyn a nie suma popraw. Zawsze zobacz że masz liczby większe od −6 i mniejsze od −2
czyli ostateczny wynik i przedział?
9 cze 05:28
ZKS:
Z miasta mistrzów Płocka (oczywiście o mistrzów mi chodzi piłkę ręczną)
9 cze 05:29
Daniel: mhmm stawiam na <−6,−2>
9 cze 05:30
Daniel: no rozumiem ja z Zamościa
9 cze 05:30
ZKS:
To już nie stawiaj tylko tak mów że jest
Trochę daleko od Płocka jak tak.
9 cze 05:33
ZKS:
Masz coś jeszcze ze tej dziedziny czy mam Ci sam coś pozadawać?
9 cze 05:33
Daniel: mhmm może tak z grubsza Miejsce Zerowe?
9 cze 05:35
ZKS:
Mam ja Ci coś dać z miejsc zerowych czy masz coś?
9 cze 05:36
Daniel: a możesz dać na początek coś łatwiejszego
9 cze 05:38
ZKS:
Znajdź miejsca zerowe funkcji :
y = 3x , y = 4x − 4 , y = x + 3 , y = √3x − 6√6 , y = 4x − 2√2x − 1
9 cze 05:41
ZKS:
Oblicz miejsca zerowe
−3x + 4 dla x < 1
f(x) =
2x − 1 dla x ≥ 1
9 cze 05:44
Daniel: y=3x
7x=0//:7
x=0
Y=4x − 4
4x − 4 = 0
4x = 4//:4
x=1
y=x+3
x+3=0
x=−3
9 cze 05:45
Daniel: z Pierwiastkami nie zrobie
9 cze 05:45
ZKS:
A dlaczego nie zrobisz z pierwiastkami spróbuj.
9 cze 05:47
ZKS:
Funkcja liniowa y = ax+ b jest malejąca i jej miejscem zerowym jest liczba niedodatnia. Ustal
znak wyrażenia a+ b .
9 cze 05:48
Daniel: −3x + 4 dla x < 1
f(x) =
2x − 1 dla x ≥ 1
Dla x<1
−3x + 4 =1
−3x = −3//:(−3)
x =1
Dla x≥1
2x−1=1
2x=2//:2
x=1
9 cze 05:51
ZKS:
Ostatecznie podaj miejsca zerowe.
9 cze 05:53
Daniel: 1 nie jest miejscem zerowym a druga jest
9 cze 05:53
ZKS:
Czemu −3x + 4 = 1 ? Tak samo w 2x − 1 = 1 ?
9 cze 05:54
Daniel: <2,−1> ? nie jestem pewien
9 cze 05:54
ZKS:
−3x + 4 = 0 dla x < 1
2x − 1 = 0 dla x ≥1
9 cze 05:55
Daniel: Miało być troszke inaczej ale to umiem
9 cze 05:55
ZKS:
Mam nadzieje że to umiesz bo tutaj pokazałeś trochę coś innego
9 cze 05:56
Daniel: wiem
9 cze 05:56
Daniel: to co ? To by było na tyle tak?
9 cze 05:57
ZKS:
| | ⎧ | −2x − 4 dla x≥0 | |
| f(x) = | ⎨ | |
|
| | ⎩ | x − 1 dla x<0 | |
9 cze 05:58
ZKS:
Zrób tamto powyżej jeszcze i podaj miejsca zerowe (o ile są)
Funkcja liniowa y = ax + b jest malejąca i jej miejscem zerowym jest liczba niedodatnia. Ustal
znak wyrażenia a + b .
Oblicz miejsca zerowe jeszcze tych
y = √3x − 6√6 , y = 4x − 2√2x − 1
9 cze 06:01
Daniel:
Dlax≥0
−2x−4=0dla x ≥0
−2x=4//(−2)
x=−2
Dla x<0 x−1=0 dla x<0
x=1
Miejsce zerowe to <−2,0>
9 cze 06:02
Daniel: NIe zrobie tego z pierwiastkami nie potrafie
9 cze 06:03
Daniel: a to tekstowe to jak to zacząc
?
9 cze 06:04
ZKS:
Dla x ≥ 0 miejsce zerowe wychodzi −2 więc nie jest miejscem zerowym!
Dla x < 0 miejsce zerowe wychodzi 1 więc nie jest miejscem zerowym!
9 cze 06:04
ZKS:
Za chwilę te tekstowe zrobimy ale najpierw pierwiastki zrób tak jak zawsze liczysz miejsca
zerowe i po kłopocie
9 cze 06:05
Daniel: Musze wolniej zadania robic bo nie zauważam drobnych rzeczy
9 cze 06:06
ZKS:
Pamiętaj o tym bo to jest bardzo ważne!
To teraz pierwiastki do dzieła
9 cze 06:08
Daniel: y=
√3x − 6
√6
√3x − 6
√6 = 0
√3x = 6
√6
√3x = 6
√6//:
√3
i tu sie moja droga kończy
9 cze 06:09
ZKS:
Ile to jest 6 : 3 ?
9 cze 06:10
Daniel: no 2
9 cze 06:10
ZKS:
Tak samo masz z pierwiastkami. Pierwiastki możesz mnożyć i dzielić przez pierwiastki.
9 cze 06:10
Daniel: x=6√2 ?
9 cze 06:11
ZKS:
To spróbuj dokończyć.
9 cze 06:11
ZKS:
Git
9 cze 06:11
Daniel: i to wszystko tyle? cy coś dalej trzeba z tym robic
9 cze 06:11
ZKS:
Zrób teraz następny przykład.
9 cze 06:12
ZKS:
Przecież wyliczyłeś miejsce zerowe to wszystko.
9 cze 06:13
Daniel: y = 4x − 2√2x − 1
4x − 2√2x − 1 =0
4x − 2√2x =1
i tu dalej tez nie wiem
9 cze 06:14
ZKS:
A wyciągnij x przed nawias.
9 cze 06:16
Daniel: oj juz zapomniałem jak sie to robi
9 cze 06:17
ZKS:
Masz jabłko * gruszka + jabłko * śliwka = (gruszka + śliwka)jabłko
9 cze 06:20
ZKS:
Widzisz mogłeś się wcześniej pouczyć to byś wszystko pamiętał
9 cze 06:20
Daniel: x(4*2√2x)=1?
9 cze 06:21
Daniel: no to zaczełem sie wczoraj uczyc o 22
9 cze 06:22
ZKS:
Nie w nawiasie nie masz mnożenia tylko dodawanie a poza tym nie wyłączyłeś x przy drugim
współczynniku
9 cze 06:24
Daniel: może omińmy ten przykład
9 cze 06:24
Daniel: x*x(4+2√2)=1 ?
9 cze 06:25
ZKS:
jabłko * gruszka + jabłko * śliwka = (gruszka + śliwka)jabłko Spójrz na to i zrób tak samo
9 cze 06:26
Daniel: No tak tylko które to które
bo sie gubie jak zaczynam to układac
9 cze 06:29
ZKS:
4x − 2√2 − 1 = 0
9 cze 06:31
ZKS:
4x − 2√2x − 1 = 0
9 cze 06:31
ZKS:
4x − 2
√2x = 1 Teraz zobacz co jest jabłkiem a co gruszką i śliwką
9 cze 06:32
Daniel: 4x * 2√2x +4*1 =(2√2x + 1)
9 cze 06:33
Daniel: Ty tutaj codziennie jesteś?
9 cze 06:34
ZKS:
Przeważnie jestem codziennie a co?
Nie 4 * x − 2√2 * x po sortuj sobie gruszki jabłka i śliwki tak jak pisałem
9 cze 06:36
Daniel: bo musze jeszcze zaliczyc Przekształcanie wektorów
9 cze 06:37
ZKS:
Zrób tamto. Ale przekształcanie wykresu funkcji o dany wektor?
9 cze 06:40
Daniel: 2x+4−2√2 =1 ?
9 cze 06:40
Daniel: tak
9 cze 06:41
ZKS:
Napisz mi które weźmiesz za jabłko a które za gruszkę i śliwkę w
jabłko * gruszka + jabłko * śliwka = (gruszka + śliwka)jabłko
9 cze 06:43
Daniel: jabłko to x gruszka to pierwiastek a sliwka to 4?
9 cze 06:44
ZKS:
Tak to teraz to zapisz ładnie.
9 cze 06:46
Daniel: ja ide sie prześpie godzinke i lece do szkoły po 15 sie odezwe
9 cze 06:46
Daniel: a to chwila juz zapisze
9 cze 06:46
Daniel: x * 2√2 + x *4 = ( 2√2 + 4)x
9 cze 06:48
ZKS:
I teraz jest wszystko dobrze.
(2√2 + 4)x = 1 Dokończ.
9 cze 06:50
Daniel: 2
√2x +4x= 6
√2x//:
√2x
2+6 +4x = 0
4x=−8 //:4
x =−2
?
9 cze 06:50
Daniel: 2√2x +4x=1
9 cze 06:51
Daniel: juz nie wiem
9 cze 06:52
ZKS:
Jak możesz dodać gruszkę i śliwkę?
(4 + 2√2)x = 1
(4 + 2√2) − to jest jakby te a we wzorze y = ax + b
9 cze 06:53
ZKS:
| | −b | |
ax + b = 0 ax = −b x = |
| |
| | a | |
9 cze 06:55
Daniel: Zaliczyłem
9 cze 21:42
ZKS:
Gratulacje skoro zaliczyłeś
10 cze 00:19
Daniel: Dzięki ZKS Jesteś?
10 cze 00:37
ZKS:
Jestem jestem. Mi dziękujesz a to czemu przecież nie pisałem tego za Ciebie.
10 cze 00:39
Daniel: Ale mnie nauczyłeś na 4 napisałem teraz pomóż mi z przekształcaniem wykresu funkcji bo o wektor
mi nie wychodzi a o osie tak
10 cze 00:40
ZKS:
A to czego nie potrafisz?
10 cze 00:42
Daniel: Napisz wzór funkcji której wykres otrzymamy , przekształcając wykres danej funkcji przez
translacje o podany obok wektor
a) f (x) = 3x u→=[2,0]
wynik powinien wyjsc y=3x+6 a mi wychodzi 3x+9
10 cze 00:44
ZKS:
A zapisz swoje obliczenia to znajdziemy błąd.
10 cze 00:46
Daniel: a robie to tak : wzor y=f(x−p)+q
Fuunkcja y=3x
Wektor: [2,0]
y=3(x+2)+3
y=3x +6+3
y=3x+9 i nie wiem co źle
10 cze 00:47
Daniel: oj powinno wyjsc 3x−6
10 cze 00:48
Daniel: Juzwiem co źle
10 cze 00:50
Daniel: y=3(x−2)+0
y=3x−6
10 cze 00:51
ZKS:
Patrz funkcję f(x) = ax i wektor u→ = [p,q] to po przekształceniu będzie to wyglądało
f(x) = a(x − p) + q tak?
Tutaj mamy wektor u→ = [2,0] czyli p = 2 a q = 0 to jak będzie wyglądała Twoja funkcja?
10 cze 00:51
ZKS:
Okej. Nie zauważyłem Twojego wyżej postu.
10 cze 00:52
Daniel: tylko teraz jak to na wykresie narysowac bo w odp. przesunął sie o 2 jednostki i nie wiem
dlaczego
10 cze 00:54
ZKS:
Przesunął się o 2 jednostki w prawo.
y = a(x − p) + q
p odpowiada za przesuwanie wykresu w lewo lub w prawo.
q odpowiada za przesuwanie wykresu w dół lub w górę.
10 cze 00:57
ZKS:
Masz taki początkowy wykres y = 3x rysujesz go najpierw a następnie przesuwasz o 2 jednostki w
prawo i otrzymujesz wykres y = 3x − 6.
10 cze 00:59
Daniel: to wiem ale z wzoru to inazej wyglada ale gdy to przerobilem przez tabelke to wyszło git czyli
wszystko rozumiem to teraz zostaje mi tylko poćwiczyc zadania
10 cze 00:59
ZKS:
Musisz się nauczyć bez rysowania tabelki bo później będziesz miał funkcję wymierna przesuniętą
o wektor a wtedy już z tabelka będzie trudno.
10 cze 01:02
ZKS:
Oczywiście dla pierwotnej funkcję rysujesz z tabelką ale później ten wykres przesuwasz o
wektor.
10 cze 01:03
ZKS:
Masz jeszcze jakieś pytania?
10 cze 01:10
Daniel: Nie juz nie Dzieki
10 cze 01:14
ZKS:
Jeżeli nie masz to pozwolisz że już pójdę się powoli kłaść. Życzę powodzenia na poprawie.
Dobranoc.
10 cze 01:17