oblicz długość odcinka x trójkąta równoramiennego ol: x−podstawa długość ramion przy podstawie po 10 kąt łączący ramiona 120 stopni

ol: ?

TPB: z tw. Carnota albo zauważ, że wysokość poprowadzona na podstawę jest również dwusieczną kąta120... wtedy już proste rachunki dla trójkąta 30,60,90.

ol: a dokładniej jak to wyliczyć? rozwiązanie

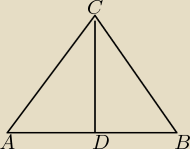
TPB: Będziemy używać oznaczeń z rysunku (to mój pierwszy na tej stronie, więc proszę o wyrozumiałość): Dane: |AC|=|BC|=10 ∡ACB = 120 st. I sposób: |AB|²=|AC|²+|BC|² − 2|AC|*|BC|*cos(∡ACB) (tw. cosinusów) Podstawiasz i otrzymujesz: |AB| = 10√3 II sposób: Zauważmy, że z faktu, że trójkąt ABC jest równoramienny wynika, że wysokość opuszczona z wierzchołka C jest dwusieczną kąta ACB.Stąd |∡ACD| = 60 st. Ponadto jest to środkowa! Trójkąt ADC jest prostokątny (to, że wysokość opada na bok pod kątem prostym jest oczywiste, takich truizmów nie trzeba tłumaczyć). Otrzymujemy trójkąt o kąta 30,60,90 i o przeciwprostokątnej równej 10. Boki AD i BD są równe, więc wystarczy wyliczyć bok AD.

	|AD|
sin(∡ACD) =
	|AC|

sin (60) = U{AD}|{10}

√3		10
	=
2		|AD

Liczysz i wychodzi: |AD| = 5√3, stąd otrzymujesz, że |AB| = 2*|AD| = 10√3 Proszę gotowiec.

ol: Łaaa.. dziękuje