W trójkącie boki mają długości Jucha: W trójkącie boki mają długości 13cm , 14 cm , 15 cm. Oblicz długość promienia okręgu, którego środek leży na najdłuższym boku, stycznego do pozostałych boków tego trójkąta

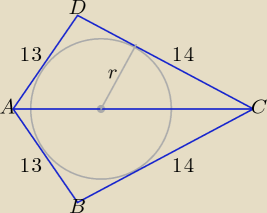
Bogdan: |AC| = 15 Zadanie sprowadza się do wyznaczenia długości promienia okręgu wpisanego w deltoid ABCD. Pole deltoidu P_d = 2*P_ΔABC. Pole trójkąta ABC można wyznaczyć z wzoru Herona, P_ΔABC = 84 ⇒ P_d = 168. Połowa długości obwodu deltoidu: p = 27 Pole dowolnego czworokąta o obwodzie 2p, w którego wpisany jest okrąg o promieniu długości r można wyznaczyć z zależności: P = p*r.

	P
Stąd r =
	p

	168		56
W tym zadaniu r =		=
	27		9

joł: π