z parametrem Nik: parametr Określ, dla jakich wartości parametru m suma kwadratów pierwiastków równania 3x² − 2mx − (m² − 1) = 0 jest najmniejsza

Nik: prosze o pomoc !

Bogdan: Najpierw założenie: Δ ≥ 0 Podaj rozwiązanie tej nierówności, potem zrobimy razem dalej.

Lajos: Δ=4m²−12m²+12= −8m²+12 Δ₂=0−4(−8)(12)=384 √Δ=4√24

	4√24
m1=
	16

	4√24
m2= −
	16

Lajos: ups nie ta strona !

Lajos: o a jednak ta czy dobrze to rozwiazalem ?

Bogdan: Nie jest dobrze, jeszcze raz wyznacz Δ i uważaj na znaki.

Lajos: ehh nie wiem gdzie jest błąd..

Kasia: Δ = 4m² + 4 * 3 * (m² − 1) = 4m² + 12m² − 12 = 16m² − 12 ...

Bogdan: Rozwiąż teraz nierówność: 16m² − 12 ≥ 0, nie stosuj Δ.

Lajos:

	6√24
m1= −
	16

	6√24
m2=
	16

Lajos:

	√12
m≥		<= o to chodziło ?
	4

Kasia:

	3
16(m2 −		) ≥
	4

	√3		√3
16(m −		)(m +		) ≥ 0
	2		2

Bogdan: Chciałbym zobaczyć, jak doszedłeś do swojego wyniku. Pokaż swoje obliczenia krok po kroku.

Lajos: patrzac na to, co napisała Kasia, moje rozwiązanie jest bezsensu

Bogdan: Kasiu − widzę, że masz ochotę rozwiązywać zadanie za Lajosa, to kontynuuj, ja wychodzę z tego wątku.

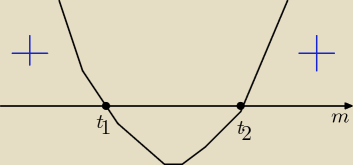
Kasia: oznaczyłam

	√3
t1 = −
	2

	√3
t2 =
	2

To teraz podaj przedział

Kasia:

	√3		√3
Δ ≥ 0 ⇔ m∊(−∞, −		>U<		, +∞)
	2		2

Lajos: kąpałem się nie mogłem odpisać dziekuje bardzo !

Kasia: To jeszcze nie koniec Zaraz napiszę drugą część tylko coś dokończę

Kasia: Część druga: x₁² + x₂² = (x₁ + x₂)² − 2x₁x₂ Wzory Viete'a to:

	b		2
x1 + x2 = −		=
	a		3

	c		−(m2 − 1)
x1 * x2 =		=
	a		3

	2		−(m2 − 1)
(x1 + x2)2 − 2x1x2 = (		)2 − 2 *		= (*)
	3		3

4		2m2 − 2
	+		/ * 9
9		3

4 + 6m² − 6 = 6m² − 2 x₁² + x₂² = 6m² − 2 Sprawdź czy dobrze obliczyłam Mogłam gdzieś się pomylić

Eta:

	2m
x1+x2=
	3

Kasia: Ajć taki błąd − <przerażona> Dzięki Eta Zaraz poprawię

Kasia: Wzory tak jak wyżej to mamy:

	b		2m
x1 + x2 = −		=
	a		3

	c		−(m2 − 1)
x1 * x2 =		=
	a		3

	2m		−(m2 − 1)
(x1 + x2)2 − 2x1x2 = (		)2 − 2(		) = (*)
	3		3

	4m2		2m2 − 2
(*) =		+		/ * 9
	9		3

4m² + 6m² − 6 = 10m² − 6 x₁² + x₂² = 10m² − 6 Eto nadal gdzieś "upadłam" ?

Kasia: Jeżeli się nie potknęłam to dokończę: Pytanie było dla jakiego m przyjmuje najmniejszą wartość − patrzymy na wykres = ma on ramiona w górę, więc jest to funkcja rosnąca. Więc wystarczy policzyć tylko x wierzchołka => x_w

	−b		0
xw =		=		= 0
	a		3

I masz odpowiedź jak się nie pomyliłam wyżej Oczywiście sprawdź czy to należy do dziedziny

Kasia: Poprawka:

	0
xw =		= 0
	10

Bogdan: Twoje rozwiązanie Kasiu zawiera błędy i nie jest poprawne. Jeśli mnożysz obustronnie przez 9, to otrzymujesz: 9(x₁ + x₂)² − 18x₁x₂ = 4m² + 6m² − 6. Ponadto nie powinno być oznaczenia x_w, bo zmienną nie jest x, a jest m.