nierówność wymierna, pierwiastek dwukrotny? Tomek: ^x2−9_x−2 > 0 Czy wynikiem w tym przypadku jest x ∊ (−∞;2), czy może x∊(−∞;−9)∪(2;9) Nie wiem, jak w nierówności traktować x²−9, czy jako x≠3 i x≠−3 i pierwiastek dwukrotny, czy normalnie rozbić x²−9 na (x−9)(x+9) i wyliczyć z tego dwa osobne pierwiastki? Nie mogę znaleźć wytłumaczenia dla takiej sytuacji.

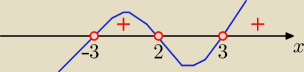
Eta: założenie:x≠2 x²−9= (x−3)(x+3)

(x−3)(x+3)
	>0
x−2

(x−3)(x+3)(x−2) >0 odp: x€ ( −3, 2) U ( 3, ∞)

Eta: https://matematykaszkolna.pl/strona/1696.html