pomocy gogoo: W trójkącie ABC dwusieczne kątów przy wierzchołkach A i B przecinają się w punkcie O. Przez punkt O prowadzimy proste równoległe do boków AC i BC, przecinające bok AB w punktach D i E. Uzasadnij, że obwód trójkąta DEO jest równy długości boku AB.

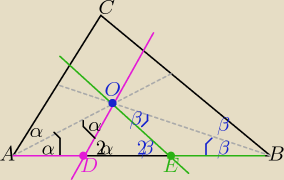
Eta: proste AB || DO => | <BAC| = | <EDO|= 2α i proste BC || EO => | <ABC| = | < DEO|= 2β to: |<DAO|= |<AOD|= α => ΔADO jest równoramienny zatem |AD|= |DO| i |<EBO|= |<BOE|= β => ΔEBO jest równoramienny zatem |EB|= |EO| Ob(ΔDEO)= |DE| +|DO|+ |EO| = |DE|+|AD| + |EB| = |AB| c.n.u.

edyta: