 1/ sprawdzamy , czy punkty M i n należą do prostej : 3x+y −2=0
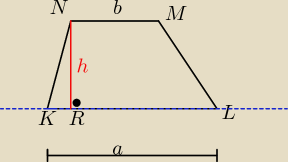
N( 2,4) to: 3*2+4 −2 ≠0 , zatem dłuższą podstawą jest |KL|= a
krótszą podstawą jest |NM|=b
z warunku zadania: |KL| = 2*|NM|
|NM|= √12+(−3)2= √10 to: |KL|= 2√10
h= d , gdzie d −−− jest odległością punktu N (2,4) od prostej : 3x+y−2=0
1/ sprawdzamy , czy punkty M i n należą do prostej : 3x+y −2=0
N( 2,4) to: 3*2+4 −2 ≠0 , zatem dłuższą podstawą jest |KL|= a
krótszą podstawą jest |NM|=b
z warunku zadania: |KL| = 2*|NM|
|NM|= √12+(−3)2= √10 to: |KL|= 2√10
h= d , gdzie d −−− jest odległością punktu N (2,4) od prostej : 3x+y−2=0
| |3*2+4*1−2| | 8 | 4√10 | ||||
d= | = | = | ||||
| √32+12 | √10 | 5 |
| a+b | ||
podstaw dane do wzoru: P= | *h=............ i dokończ obliczenia
| |
| 2 |
