obliczyc pole obszaru ograniczonego liniami alexia: y=2x−x2, x=y=0

alexia: sorry tam miało byc x+y=0

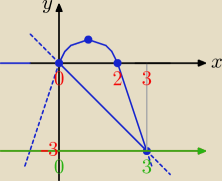
Bogdan: y = 2x − x² i y = −x Można przesunąć układ współrzędnych o 3 jednostki w dół, co jest równoznaczne z translacją wykresów y = 2x − x² i y = −x o wektor [0, 3]. Wykresy po przesunięciu wyrażają się wzorami: parabola y = −x² + 2x + 3, prosta y = −x + 3. Pole ograniczone tymi liniami można obliczyć z zastosowaniem całki oznaczonej w granicach od x = 0 do x = 3: 3 Pole P = ∫ (−x² + 2x + 3 − (−x + 3)) dx 0

alexia: dziękuję

alexia: a mam jeszcze pytanie... tą całkę się tak zostawia czy trzeba ją liczyć?

Bogdan: Jeśli polecenie w zadaniu brzmi: oblicz pole obszaru, to trzeba całkę obliczyć. W tym przypadku trzeba.

alexia: a mogłabym prosić o obliczenie jej bo chciałabym sprawdzic z tym co sama policzylam

Bogdan: Nie, ta za łatwa całka. Podaj zapis swojego rozwiązania, sprawdzę.

ICSP:

	9
Bogdam		wyjdzie?
	2

Bogdan: Przepraszam ICSP, ale poczekam na odpowiedź alexia i jej zapis obliczeń.

ICSP: ale gdybym miał źle to nie pisz poprawnej tylko ja spróbuje znaleźć błąd w swoich obliczeniach.

Bogdan: Dobrze

alexia: 3 −x² x³ ∫=2*_____ − ___ 0 2x+3 3 x²=2x+3 X²−2x−3=0 a=1 b=−2 c=−3 Δ=16 pierwiastek z Δ=4 x1=−1 x2=3

alexia: oto moje wypociny oczywiście cierpię na dyskalkulię ale to akurat z zeszytem robiłam

alexia: tam ma byc 3−X² przez 2x+3 − x³ przez 3

Bogdan: Przed wysłaniem swojego zapisu proszę sprawdzić na podglądzie, czy jest czytelny. Twój zapis alexia nie jest czytelny. Czy wiesz, jak oblicza się wartości całek oznaczonych?

alexia: ∫f(x)dx=F(b)−F(a)=F(x)^b_a

Bogdan: No właśnie, to teraz zastosuj tę formułę i pokaż swoje obliczenia.

alexia: P=^3x2₂−^x3₃ P=¹₆(9−2x)x² P=−¹₆x²(2x−9) P+^x3₃−^3x2₂=0 P=0 x=⁹₂

alexia: P=⁹₂ x=−³₂ P=⁹₂ x=3

alexia: dobrze?

Bogdan:

	9
P =
	2

	3		1		3		1
P = [F(3) − F(0)] 03 = [		x2 −		x3] 03 =		*32 −		*33 =
	2		3		2		3

	1		1
= 13		− 9 = 4
	2		2

alexia: ok, dzieki ale mam problem jeszcze z jednym zadaniem 9y2=4x3 0≤x≤3 na długość łuku

Bogdan: Widzę zadanie ze zbioru zadań Krysickiego i Włodarskiego: "Analiza matematyczna w zadaniach" (zadanie nr 20.28). Przekształć wzór linii do postaci y = ... i zastosuj procedurę wyznaczania długości łuku, jest podana w wymienionym zbiorze zadań.

alexia: nie posiadam niestety tego zbioru... czy to będzie coś takiego?: 9y²=0≤x≤3 y=0 ⋀ 0≤x≤3

Bogdan: To polecam ten zbiór. Jeszcze raz. Przekształć wzór 9y² = 4x³ do postaci y = ...

alexia: y²=^4x3₉ y=^2x3/2₃

Bogdan:

	2x3/2
Stosuj dużą literkę U przy zapisywaniu ułamków. Efekt jest taki: y =		.
	3

	2
y =		x3/2
	3

0 Długość łuku dla y ≥ 0 i x∊<0, 3> oblicz z zależności: L = ∫ √ 1 + (y')² dx 3

ICSP: Bogdan dwa pytanka. Pierwszy raz w życiu liczyłem długość łuku więc kompletnie nie jestem pewien wyniku − 12 Drugie czy jest różnica w zapisie 3 na dole czy 3 na górze w tym zapisie całki?

ICSP: oczywiście 12 jest na plusie.

alexia:

	ϱ		4
2 ∫p{1		√		x3dx
	ϱx		9

tam po całce oczywiscie jest pierwiastek, wszystko jest pod duzym pierwiastkiem i ten symbol ϱ oczywiscie jest inny ale nie było podobnego

alexia: 6√3≈10,392 tak ma wyglądać wynik?

Bogdan: b a ICSP, Jest różnica w zapisach ∫ f(x) dx, ∫ f(x) dx. a b 3 W tym przypadku powinno być L = ∫ √1 + (y')² , mój poprzedni zapis nie jest właściwy, 0 nawet nie zauważyłem wysyłając go, że chochlik coś namieszał. Dziękuję ICSP za zwrócenie uwagi na ten szczegół. 12, a także 6√3 nie są poprawnymi rozwiązaniami.

alexia: to ja już nie wiem...poddaje się

Bogdan:

	2		2		3
y =		x3/2, y' =		*		x1/2 = √x, (y')2 = x
	3		3		2

	t3/2
∫ (1 + x)1/2 dx = / 1 + x = t, dx = dt / = ∫ t1/2 dt =		+ C =
	3/2

	2
=		(1 + x)√1 + x + C
	3

Długość łuku L dla y ≥ 0 i x∊<0, 3>:

	2		16		2		14
L = [		(1 + x)√1 + x ]03 =		−		=
	3		3		3		3

alexia: dzięki

ICSP: Bogdan mam pytanko

	2
∫ √1+xdx =		(x+1)32 + C czy to jest źle obliczone?
	3

ICSP: Nie ja genialny jestem Liczyłem tak:

2
	* (x+1)32 . teraz wstawiamy 3
3

2
	* 8 = 12 Jak ja maturę zdałem
3

2		16
	* 8 =		ale nadal mi źle wychodzi:(
3		3

ICSP: a nie przepraszam bardzo. Już znalazłem błąd. Dziękuję Bogdanie

Bogdan: ICSP, teraz do swojego wyniku wstaw 0, bo przedział jest od 0 do 3.

ICSP: zauważyłem właśnie Zmyliło mnie liczenie całek z zerem na dole i zapomniałem że 1ⁿ = 1

naten: Obliczyć pola obszaru ograniczonego parabolami y=4−x2 oraz y=x2−2x