Przedział, zbiór rozwiązań Golibroda: Proszę o pomoc w dwóch zadaniach. 1.Wskaż nierówność która opisuje przedział (2;6) A. Ix−4I < 2 B. Ix−3I <4 C. Ix−4I < 3 D. taka sama jak C czyli pewnie jakiś błąd wydrukowany. Mi wychodzi w A (6;2) i wydaje mi się ze to to samo co (2;6) ale nie wiem. 2. Zbiorem rozwiązań nierówności −x² ≥ 81x jest przedział: A. <0;81> B. <−9;9> C. <−81; 0 > D. (−9;0) Jak dojść do rozwiązania? bo coś mi nie pasuje ten x przy 81 będę wdzięczny za pomoc.

ICSP: nie ma czegoś takiego jak (6;2) liczby w zbiorach zapisujemy od mniejszej do większej −x² ≥ 81x ⇔ x² + 81x ≤ 0 ⇔ x(x+81) ≤0 ⇔ x ∊ <−81;0>

marmar: A. x − 4 < 2 ∧ x − 4 > −2 x < 6 ∧ x > 2 x ∊ (2,6) odp A!

Golibroda: OK, dzięki za pomoc.

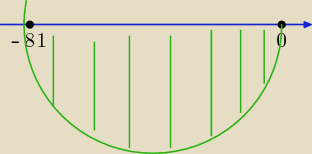
PanCogito: 2. −x² ≥ 81x ⇒ x²+81x ≤ 0 ⇒ x(x+81) ≤ 0 Mamy dwa miejsca zerowe : x₁ = 0 x₂ = −81 x ∊ <−81; 0>