 1. Na okręgu opisano trapez równoramienny. Kąt rozwarty trapezu ma miarę 150 stopni, a odcinek
łączący środki ramion ma 12 cm długości. Oblicz długość promienia okręgu.
2. Na okręgu opisano trapez, którego obwód wynosi 52 cm. Oblicz długość odcinka łączącego
środki rmion tego trapezu.
3. W trapezie równoramiennym podstawy mają długość 25 cm i 7 cm, a przekątna ma długość 20 cm.
Oblicz odległość punktu przecięcia przekątnych od obu podstaw.
1. Na okręgu opisano trapez równoramienny. Kąt rozwarty trapezu ma miarę 150 stopni, a odcinek
łączący środki ramion ma 12 cm długości. Oblicz długość promienia okręgu.
2. Na okręgu opisano trapez, którego obwód wynosi 52 cm. Oblicz długość odcinka łączącego
środki rmion tego trapezu.
3. W trapezie równoramiennym podstawy mają długość 25 cm i 7 cm, a przekątna ma długość 20 cm.
Oblicz odległość punktu przecięcia przekątnych od obu podstaw.
| 5 | 3 | |||
3. 2 | cm, 9 | cm | ||
| 8 | 8 |
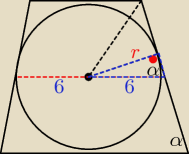 Teraz miara kąta ostrego α wynosi 180−150=30 stopni
Przerysuję ten mały niebieski trójkącik w następnym poście
Teraz miara kąta ostrego α wynosi 180−150=30 stopni
Przerysuję ten mały niebieski trójkącik w następnym poście 
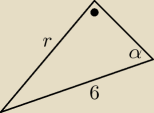 α=30 stopni, więc z zależności trygonometrycznej:
α=30 stopni, więc z zależności trygonometrycznej:
| r | ||
sinα= | ||
| 6 |
| 1 | r | ||
= | , więc: | ||
| 2 | 6 |

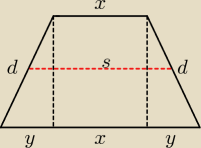 Z warunku, że okrąg jest wynika, że:
x+x+y+x=d+d
2x+2y=2d
d=x+y
Z warunku, że okrąg jest wynika, że:
x+x+y+x=d+d
2x+2y=2d
d=x+y
| x+x+y+y | ||
Odcinek łączący śr. ramion: s= | =x+y | |
| 2 |




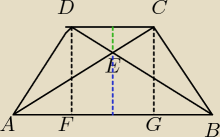 |FG| = |DC| = 7
|AF| = |GB|
2|AF| + |FG| = 25 ⇔ 2|AF| = 18 ⇔ |AF| = 9
|FG| + |GB| = 16
Z trójkąta DFB:
|DF| = h
Na oko widać ze jest to trójkąt egipski( zwany również Pitagorejskim) dlatego h = 12. Jeżeli
nie znasz własności trójkątów egipskich musisz liczyć h z twierdzenia Pitagorasa.
Teraz oznaczamy :
zielony docinek = x
niebieski odcinek = y
x + y =12
∡AEB = ∡DEC
∡EAB = ∡ECD
∡ABE = ∡CED
|FG| = |DC| = 7
|AF| = |GB|
2|AF| + |FG| = 25 ⇔ 2|AF| = 18 ⇔ |AF| = 9
|FG| + |GB| = 16
Z trójkąta DFB:
|DF| = h
Na oko widać ze jest to trójkąt egipski( zwany również Pitagorejskim) dlatego h = 12. Jeżeli
nie znasz własności trójkątów egipskich musisz liczyć h z twierdzenia Pitagorasa.
Teraz oznaczamy :
zielony docinek = x
niebieski odcinek = y
x + y =12
∡AEB = ∡DEC
∡EAB = ∡ECD
∡ABE = ∡CED
| y | 25 | |||
Z tego wynika ze ΔABE jest przystający do ΔDEC czyli | = | ⇔ 25x = 7y | ||
| x | 7 |
| 3 | ||
y = 9 | ||
| 8 |
| 5 | ||
x = 2 | ||
| 8 |
| y | 25 | |||
Z tego wynika ze ΔABE ∼ ΔDEC czyli | = | ⇔ 7y = 25x. | ||
| x | 7 |


 Poleciałem z proporcji a potem Pitagoras
Poleciałem z proporcji a potem Pitagoras 

 teraz tylko 2 nie rozumiem.. moglby mi ktos to jakos w
prostszy sposob rozpisac? bardzo prosze..
teraz tylko 2 nie rozumiem.. moglby mi ktos to jakos w
prostszy sposob rozpisac? bardzo prosze.. z góry dziękuje za pomoc bo ja tego nie rozumiem
z góry dziękuje za pomoc bo ja tego nie rozumiem
