dlugosci bokow trojkata prostokatnego tworza ciag arytmetyczny o roznicy1. oblic
dani 3612: dlugosc bokow trojkata prostokatnego tworza ciag arytmetyczny o roznicy 1.oblicz dlugosc
przeciw prostokatnej tego trojkata
3 cze 16:52
asd:
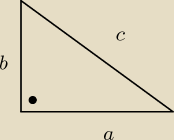
a
2 + b
2 = c
2
ciąg arytmetyczny
c − bok najdłuzszy
a − najkrutszy
c = a + 2
b = a + 1
podstawiamy do wzoru a
2 + b
2 = c
2
a
2 + (a+1)
2 = (a+2)
2
a
2 + a
2 + 2a + 1 = a
2 + 4a + 4
a
2 − 2a − 3 = 0
mamy równanie kwadratowe.
ważne sa załozenie ze wszystkie boki muszą być większe od zera
a>0
b>0
c>0
równanie kwadratowe
−−−−−−−> a
2 − 2a − 3 = 0
Δ = 4 + 12 = 16
√Δ =
√16 = 4
a
1 =
2+42 = 3
a
2 =
2−42 = −1
a
2 odpada bo a musi być >0.
a=3
b=4
c=5
Odp. Dane było poszukać tylko przeciwprostokątnej czyli c = 5
3 cze 17:30
leszcz:
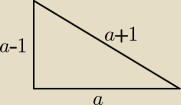
(a − 1)
2 + a
2 = (a + 1)
2, a > 0
a
2 − 2a + 1 + a
2 = a
2 + 2a + 1
a
2 − 4a = 0
a(a − 4) = 0
a = 0 lub a = 4 i a − 1 = 3 i a + 1 = 5
3 cze 19:03
dani 3612: wykaz ze ciag an okreslony wzorem an=2pod kreska n+1 jest malejacy
3 cze 19:23