bok rombu ma dł. 4 cm , a suma przekątnych jest równa 10 cm. oblicz pole i wyso
xyz: bok rombu ma dł. 4 cm , a suma przekątnych jest równa 10 cm. oblicz pole i wysokość rombu.
2 cze 16:29
M:
15 mar 06:16
Mariusz:
Z twierdzenia cosinusów
d
12 = 4
2+4
2 − 2*4*4*cos(α)
d
22 = 4
2+4
2 + 2*4*4*cos(α)
Dodając stronami
d
12+d
22 = 64
d
12+d
22 = (d
1+d
2)
2−2d
1d
2
10
2 − 2d
1d
2 = 64
2d
1d
2 = 36
P = 9 cm
2
15 mar 08:45
Mei Lin:
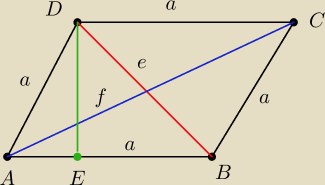
a=4
e+f=10
W dowolnym czworokącie zachodzi
a
2+b
2+c
2+d
2=e
2+f
2+4m
2
m−odległośc miedzy środkami przekątnych
W rombie m=0
4a
2=e
2+f
2
4*4
2=(e+f)
2−2ef
64=100−2ef
2ef=36
e*f=18
P=a*h
czyli tak jak u Mariusza .
15 mar 14:57
rombek:
| | fe | |
f+e=10 f2+e2=4a2 i P= |
| ⇒ 4P=2fe |
| | 2 | |
f
2+e
2=(f+e)
2−2fe
10
2−4P=64
4P=36
P=9
15 mar 17:48
kantek:
15 mar 20:23