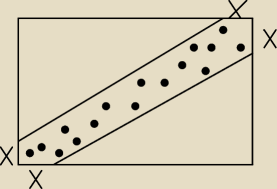
funkcja rrr: Bardzo proszę o pomoc w rozwiązaniu zadań. Zad 1) Szerokość pokoju jest o 2 m mniejsza od jego długości . Jakie wymiary może mieć ten pokój, jeśli przekątna podłogi jest nie mniejsza od 6 m i nie większa od 10 m? Zad 2) Boki prostokąta mają długości 8 i 10. Dla jakich wartości x zacieniowany obszar stanowi co najmniej 40% powierzchni prostokąta rys do zad 2

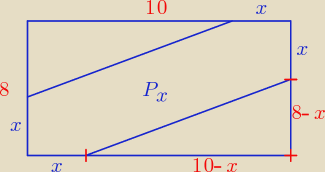
Godzio: P = 8 * 10 = 80 40%P = 32 P_x ≥ 32 x ∊ (0,8)

	(10 − x)(8 − x)
P − 2 *		≥ 32
	2

80 − (80 − 18x + x²) ≥ 32 − x² + 18x − 32 ≥ 0 x² − 18x + 32 ≤ 0 Δ = 324 − 128 = 196 √Δ = 14 x₁ = 2, x₂ = 16 ⇒ x ∊ <2,16> + D ⇒ Odp: x ∊ <2,8)

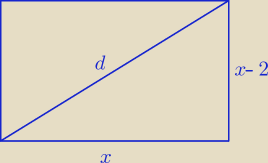
Godzio: 6 ≤ d ≤ 10 /² 36 ≤ d² ≤ 100 36 ≤ x² + (x − 2)² ≤ 100 x > 2 36 ≤ 2x² − 4x + 4 ≤ 100 /:2 18 ≤ x² − 2x + 2 ≤ 100 0 ≤ x² − 2x − 16 i x² − 2x − 98 ≤ 0 Rozwiąż te dwie nierówności i podaj część wspólną

rrr: dziękuje bardzo ale prośiłbym o rozwiazanie tego zadania do końca ,nie zgadza się odpowiedz chyba tak powino być x²−2x−16≥0 i x²−2x−48≤0

Godzio: No powinno Nie podzieliłem 100 przez 2 2x² − 4x + 4 ≤ 100 /:2 x² − 2x + 2 ≤ 50 x² − 2x − 48 ≤ 0

rrr: w zad 1 odp .w podręczniku jest x∊< √17 −1,6 >

rrr: mam prośbę niech pan to wyliczy bo też otrzymałem taką samą odp. jak pana

Godzio: 0 ≤ x² − 2x − 16 Δ = 4 + 64 = 68 √Δ = 2√17 x₁ = 1 + √17 x₂ = 1 − √17 x ∊ (−∞,1 − √17> U <1 + √17,∞) x² − 2x − 48 ≤ 0 Δ = 4 + 192 = 196 √Δ = 14 x₁ = 8 x₂ = −6 x ∊ <−6,8> Część wspólna: x ∊ <1 + √17, 8> Odp z podręcznika jest błędna, wystarczy wziąć: 4 (która mieści się w tym przedziale) i otrzymujemy: d² =(x − 2)² + x² d² = 4 + 16 d = √20 ≈ 4,47 więc nie spełnia założeń zadania

rrr: jeszcze raz bardzo dziękuje

dhgkdj: W podr jest dobra odpowiedz. Kwestia tego czy dales na rysynku x+2 i x czy x−2i x