promien okregu opisanego na trojkacie
Ola: Jak znaleźć długość promienia okręgu opisanego na dowolnym trójkącie ? (nie korzystając z
twierdzenia sinusów), tzn. dochodząc do tego samemu.
1 cze 19:47
krystek: czy konstrukcyjnie?
1 cze 19:49
Ola: nie konstrukcyjnie, konkretnie.
1 cze 19:56
ICSP: ze wzoru na pole.
1 cze 19:58
Godzio:
Chodzi Ci o wyprowadzenie wzoru na promień okręgu opisanego bez twierdzenia sinusów ?
1 cze 20:00
Ola: tak Godzio, o to mi chodzi

1 cze 20:01
Ola: PONAWIAM

1 cze 21:50
Godzio:
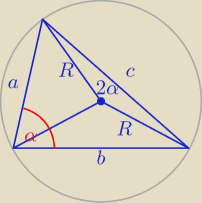
R
2 + R
2 − 2R
2cos2α = c
2
2R
2(1 − cos2α) = c
2
| c2 | |
| = 1 − (1 − 2sin2α) |
| 2R2 | |
| c2 | | c | |
| = 2sin2α ⇒ sinα = |
| |
| 2R2 | | 2R | |
| | 1 | | c | | abc | |
P = |
| ab * |
| ⇒ R = |
| |
| | 2 | | 2R | | 4P | |
1 cze 22:01
Bogdan:
Godzio − spróbuj wyznaczyć R bez korzystania z twierdzenia cosinusów.
1 cze 22:08
Godzio:
Ok, zaraz pomyślę

1 cze 22:08
Godzio:
Jeszcze dopytam, mam wyznaczyć R w zależności od a,b,c i P czyli doprowadzić do tego wzoru:
1 cze 22:12
Bogdan:
| | a | | abc | |
Możesz doprowadzić do zależności: R = |
| albo R = |
| wychodząc |
| | 2sinα | | 4P | |
z twierdzenia o kącie wpisanym i środkowym opartych na tym samym łuku i z elementarnych
funkcji trygonometrycznych w trójkącie prostokątnym.
1 cze 22:18
Godzio:
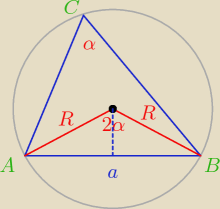
1 cze 22:22
Bogdan:
| | abc | |
No właśnie Godzio, idź za ciosem i doprowadź do zależności R = |
| |
| | 4P | |
1 cze 22:23
Godzio:
| | 1 | |
Korzystając z : P = |
| bcsinα |
| | 2 | |
Ale domyślam się, że nie ma tak łatwo, dlatego muszę chwilkę pomyśleć

1 cze 22:29
Godzio:
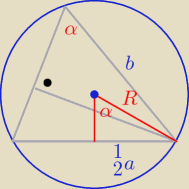
Wymyśliłem

Z podobieństwa:
1 cze 22:36
Godzio:
| | R | |
Oczywiście miało być: |
| |
| | b | |
1 cze 22:37
Bogdan:
Brawo
Godzio 
1 cze 22:47






 Wymyśliłem
Wymyśliłem  Z podobieństwa:
Z podobieństwa:
