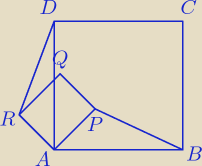
dowód Kasia: Czworokąty ABCD i AP QR są kwadratami. Udowodnij, że |BP| = |DR|

Kasia: Pomocy

ICSP: |RA| = |PA] |AD| = |AB| z tego wynika że Δ APB jest przystający do Δ ARD a zatem |PB| = |RD| c.n.u.

Kasia: na jakiej podstawie? bbb?

Kasia: A nie można by udowodnić to tak: Trójkąty △ABP i △ADR są przystające. Kwadrat posiada kąt 90^o, więc: W trójkącie △ABP: ∡DAP = 90^o − ∡BAP W trójkącie △ADR: ∡DAR = 90^o − ∡DAP = 90^o − (90^o − ∡BAP) = ∡BAP czyli ∡DAR = ∡BAP i dokończyć tylko boki i mamy: na podstawie bkb