Proszę o pomoc w 2 zadaniach Andrzej:

	1		1		3
Zbuduj kątα taki że: sinα=		cosα=		tgα=
	2		2		4

1
2

oraz zadanie 2: Oblicz wartość wyrażenia A) sin²45+cos²135 B)tg135stopni−ctg225stopni= C) sin135stopnicos225stopni ____________________ tg²135stopni− ctg²90 stopni D) cos330 stopni+tg10 stopnictg300stopni Proszę o jakieś nie skomplikowane rozwiązania ( całkiem padam w trygonometrii )

Anna: No to rysujemy.

Andrzej: ja jestem ciemny z tego muszę się ogólnie wsiąść w garść za trygonometrie Bd jutro pisał poprawkę z tych zadań a ciemny jestem.

Anna:

	1
sinα =
	2

	1		3
Ułamek		rozszerzymy np. na		. Nie jest to konieczne, ale będzie Ci łatwiej z
	2		6

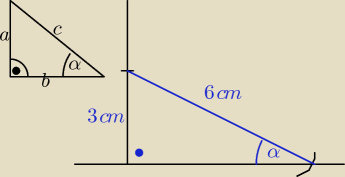
jednostkami. Narysujemy rysunek pomocniczy, w którym zaplanujemy położenie kąta α. Np. tak jak na rys. powyżej.

	a		a		3
Z definicji: sinα =		. Czyli		=		, stąd a=3cm, c=6cm. (jednostka
	c		c		6

dowolna) Teraz rysujesz linię prostą, z dowolnego jej punktu rysujesz prostą prostopadłą (można konstrukcyjnie lub na kratkach). Na tej prostopadłej odmierzasz odcinek 3cm. Teraz cyrklem odmierz odcinek 6cm (narysowany np. gdzieś na boku) i z górnego końca tego odcinka prostopadłego zakreśl łuk przecinający pierwszą prostą. Ten punkt przecięcia łuku z prostą będzie wierzchołkiem szukanego kąta α..Wystarczy połączyć otrzymany punkt z górnym końcem odcinka a i gotowe. Spróbuj i napisz, jak poszło. Tymczasem napiszę Ci zad. 2.

Anna: A Ty znasz wzory redukcyjne? One są tylko na poziomie rozszerzonym.

Anna:

	√2
A) sin2450 + cos21350 = (		)2 + [cos(900+450)]2=
	2

	2		1		√2		1		1
=		+ [−sin450]2=		+ (		)2 =		+		= 1
	4		2		2		2		2

Anna: B) tg135⁰ − ctg225⁰ = tg(90⁰+45⁰) − ctg(180⁰+45⁰) = = −ctg45⁰ − ctg45⁰ = −2ctg45⁰ = −2*1= −2

Anna: C) Obliczę każdy czynnik osobno, potem podstawię.

	√2
sin1350 = sin(900+450) = cos450 =
	2

	√2
cos2250 = cos(1800+450) = − cos450 = −
	2

tg135⁰ = tg(90⁰+45⁰) = − ctg45⁰ = −1 ctg90⁰ = 0 Po podstawieniu mamy:

√2   √2   *(− ) 2   2		1   −   2		1
	=		= −
(−1)2 − 02		1		2

Anna: W zad. 2 d) jest na pewno tg10⁰ ?

Andrzej: srki jest rg 120stopni

Andrzej: *tg

Andrzej: właśnie nie znam wzorów redukcyjnych A Anniu nie da się troszkę innym sposobem napisać to 2?