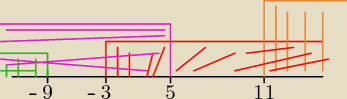
PROblem TOmek: Przypominam sobie działy wart. bezwzględna miałem zadanko ||x−1|−7>3 wyszło mi x>11 v x<−9 x<5 x>−3 to jest dobrze ,zaznaczam na osi i co tu jest rozwiązaniem

Godzio: x ∊ (−∞,−9) U (−3,5) U (11,∞) Jeśli tak Ci wyszło to ok, trzeba pamiętać o sumie i części wspólnej żeby tego nie pomieszać

TOmek: czyli odpowiedzią ,jest to gdzie conajmniej 2 "bloki" sie nakrywają? yes?

Godzio: Nie zawsze musi tak być chyba, ale w tym wypadku tak

Godzio: | |x − 1| − 7 | > 3 |x − 1| − 7 > 3 lub |x − 1| − 7 < − 3 |x − 1| > 10 lub |x − 1| < 4 (x − 1 > 10 lub x − 1 < − 10) lub (x − 1 < 4 i x − 1 > − 4 ) (x > 9 lub x < − 9) lub (x < 5 i x > − 3 ) suma część wspólna suma

Godzio: x > 11 oczywiście

TOmek: a gdyby wszystkie sie nakrywały w jakimś miejscu, to wtedy tylko ten odcinek był by rozwiązaniem, (nie wiem czy zrozumiesz to co napisałem

Godzio: To zależy od tych znaków "lub" i "i"

TOmek: aha juz wiem od czego to zalezy, musze poszukac stare notatnki, akurat wart. bezwzględa moze byc na przyszłorocznej maturze, a ten dział troche odpusciłem

TOmek: dzieki za przypomnienie