Planimetria Majeczka: Oblicz długości odcinków: AB, BC i AC. Czy punkty A, B, C są współliniowe? a) A(−4, 5), B(0, 2), C(8, −4) O ile pierwsza część zadania wydaje mi się łatwa, to problem pojawia się w drugiej części. O co chodzi z tą współliniowością?

ge:

aniabb: liczysz prostą z dwóch punktów i sprawdzasz czy trzeci pasuje do tej prostej

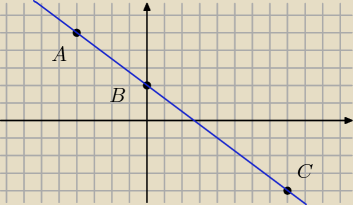
aniabb: tak są współliniowe

niger: δδδδδδ

julka:

Jolanta: |AB|=√(x_B−x_A)²+(y_B−yA)²=√(0+4)²+(2−5)²=√16+9=√25=5 Pozostałe długości w ten sam sposób podstawiając odpowiednie współrzędne Wzór na prosta y=ax+b A (−4,5). B(0,2) 5=−4a+b 2=0+b 5=−4a+2 3=−4a a=−3/4 y={−3}{4}x+2. C(8,−4)

	−3
−4=		*8+2
	4

−4=−6+2 −4=−4 punkt C leży na tej samej prostej co A i B Są współliniowe

aa: a) wystarczy obliczyć współczynniki kierunkowe ( bez wyznaczania równania prostej)

	2−5		3		−4−5		3
aAB=		= −		i aAC=		= −
	0+4		4		8+4		4

wniosek : punkty A,B,C są współliniowe

bb:

aa: Pozdrawiam bb