Planimetria Majeczka: PROSZĘ O POMOC: Odcinek AC jest średnicą okręgu o promieniu 2. Cięciwa AB tego okręgu ma długość 2√3. Wyznacz miarę kąta między cięciwą AB i styczną do okręgu w punkcie B oraz miarę kąta między cięciwą BC i styczną do okręgu w punkcie C.

Majeczka: Pomoże ktoś?

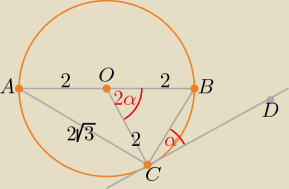
Bogdan: Kąt wpisany AOC jest półpełny, więc oparty o ten sam łuk kąt ABC jest prosty, stąd trójkąt ABC jest prostokątny. Korzystając z twierdzenia Pitagorasa obliczamy |BC| = √16 − 12 = 2, a więc trójkąt BOC jest równoboczny. Korzystając z twierdzenia o kącie dopisanym otrzymujemy: |∡BOC| = 2|∡BCD| Przeanalizuj te informacje i podaj odpowiedzi.