Proszę o pomoc! Nie wiem jak się za to zabrać kinga: W trójkącie ABC przeprowadzono dwusieczną kąta C a następnie narysowano prostą m prostopadłą do tej dwusiecznej, która przecięła boki AC i BC trójkąta odpowiednio w punktach Ei F. wykaż że trójkąt EFC jest równoramienny. Tu jest też rysunek zadanie 24. http://www.speedyshare.com/files/28669991/matma.jpg

tn: dwusieczna dzieli kąt na dwa równe −> połowy zatem kąty OCE i FOC są równe powiedzmy α również kąty FCO oraz ECO są równe bo są proste i mają po 90 stopnie zatem katy CFO oraz CEO są równe. Są to kąty przy podstawie, jeśli są równe to trójkąt jest równoramienny, myślę że takie cos wystarczy

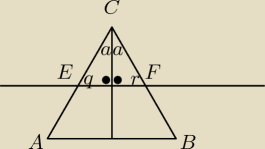
tn: kąty a są równe, są równymi połowami na które podzieliła je dwusieczna q+90+a=180 q+a=90 q=90−a zaś r r+90+a=180 r+a=90 r=90−a ⇒ r=q ⇒kąty przy podstawie mają równą miarę ⇔ trójkąt jest równoramienny c.k.d