?? simon: oblicz wysokosc i przekątną trapezu rownoramiennego o podstawach 21cm i 11cm oraz ramieniu 13

oaxoaxoax:

	21−11
x=		=5
	2

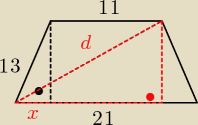
5² + h² = 13² h²=144 h=12 (21+5)² + 12² = d² 400=d² 20=d

oaxoaxoax: Zapomniałem oznaczyć h, ale to łatwo się domyślić .

simon: dzieki wielkie

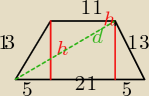
tn: 5² + h² = 13² h=12 d² = 26² + 12² d = √820 = 2√205

tn: aj, pomyliłem sie przy przekątnej

tn: ale przecież 26² + 12² = 820 a nie 400

simon: yyyyhhh to ktorej jest dobre wkoncu?

oaxoaxoax: tn, a moze zauwazysz, ze to cala podstawa ma 21, wiec 21−5=16 bo odjelismy x ( patrz moj rysunek)

oaxoaxoax: tn, a moze zauwazysz, ze to cala podstawa ma 21, wiec 21−5=16 bo odjelismy x ( patrz moj rysunek)

simon: no widze ale tu sa dwa rozwiazania ktore dobre?

oaxoaxoax: Moje jest prawidlowe. Kolega sie machnal .

oaxoaxoax: Tez sie machnalem, przepraszam. Powinien byc zapis 21−6 i potem jest ok

oaxoaxoax: 21−5* pomylka bo pisze z telefonu :x

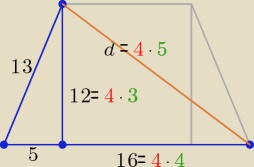
Bogdan: Znany jest trójkąt egipski o bokach długości: 3, 4, 5 (3² + 4² = 5²)

simon: no dobra spoko dzieki za wszystko

Bogdan: W zadaniach maturalnych z poziomu podstawowego, a także w zbiorach zadań z tego poziomu występują w zadaniach z trójkątami prostokątnymi najczęściej trójkąty o bokach długości 3, 4 i 5 (względnie wielokrotności tych liczb: 6, 8, 10 lub 9, 12, 15 lub 12, 16, 25 itd) oraz trójkąty o bokach długości 5, 12 i 13 (względnie wielokrotności tych liczb: 10, 24, 26 lub 15, 36, 39 itd.).

simon: