metoda stycznych PROSZE O POMOC !!! Jacek: Bardzo prosze o pomoc z jednym zadankiem od godziny proboje je zrobic i mi nie wychodzi. x³+x−1=0 przedzial [0,5 ; 2] wyznaczyc przyblizony pierwiastek rownania przeprowadzajac 3 iteracje metody siecznych

Godzio:

	1
f(x) = x3 + x − 1 [		, 2]
	2

	1		1		1		3
f(		) =		+		− 1 = −
	2		8		2		8

f(2) = 8 + 2 − 1 = 9

	f(xn)
xn + 1 = xn −		(2 − xn)
	f(2) − f(xn)

	1		3   −   8		1		1		3		3
x1 =		−		(2 −		) =		+		*		=
	2		3   9 +   8		2		2		75		2

	1		3		28
=		+		=		= 0,56
	2		50		50

f(x₁) = −0,264384

	f(x1)		0,264384
x2 = x1 −		(2 − x1) = 0,56 +		(2 − 0,56)
	f(2) − f(x1)		9 + 0,264384

x₂ ≈ 0,601094 f(x₂) ≈ −0,181722

	f(x2)
x3 = x2 −		(2 − x2)
	f(2) − f(x2)

	0,181722
x3 = 0,601094 +		(2 − 0,601094) ≈ 0,628781
	9 + 0,181722

Sprawdzaj obliczenia bo mogłem się gdzieś walnąć

Jacek: pierwsza iteracja wyszla mi tak samo, ale potem nie rozumiem za bardzo ja robilem tak ze w drugiej iteracji x2= 0,56 − (f(0,56)*(0,56−2)/f(0,56)*f(2)) wedle wzoru metody stycznych A ty jakos poprzestawiales tam (tobie dobrze wyszlo ) tylko czemu tak sie robi

Jacek: ajj oczywiscie metody siecznych nie stycznych literowka

Godzio: Chodzi Ci czemu podstawia się kolejne przybliżone pierwiastki ?

Jacek: chodz mi o to czemu w 2iteracji na przyklad : masz f(2)−f(x1) i (2−x1) wedle wzoru powinno byc f(x1)−f(2) i (x1−2)

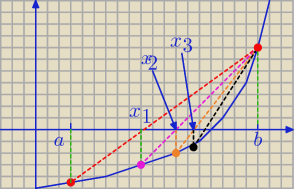
Godzio: No właśnie nie, wartość w dwójce jest stała i to przez nią przechodzą wszystkie sieczne W przypadku, gdy f(a)<0 koniec b przedziału <a, b> jest nieruchomy

Jacek: Czyli zle nas uczono... dziekuje bardzo za pomoc