Trudne Sławek: Graniastosłup prawidłowy trójkątny, którego wszystkie krawędzie są równej długości, ma pole powierzchni całkowitej równe 18+3√3. Oblicz objętość tego graniastosłupa. Pozdrawiam!

Bogdan: Bez przesady z tą trudnością. Z jakich ścian zbudowany jest ten graniastosłup?

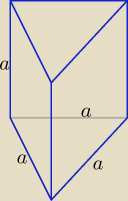
Bogdan: Ściany to jak widać 3 kwadraty i 2 trójkąty równoboczne.

	1
3a2 + 2*		a2√3 = 18 + 3√3 stąd a2 = ... i a = ...
	4

	1
Objętość V =		a2√3 * a
	4

Sławek: ok. ale skąd wziąść to a właśnie?

Godzio: Trzeba wyznaczyć z równania:

	1
3a2 + 2 *		a2√3 = 18 + 3√3
	4

Sławek: a mógłbyś mi rozpisac jak to wyznaczyc z tego równania? Ja jestem zielony z matmy. Jakbym nie było to bym tu nie pisał

Godzio:

	1
3a2 +		a2√3 = 18 + 3√3 / * 2
	2

6a² + √3a² = 36 + 6√3 a²(6 + √3) = 36 + 6√3 a² = ... Dalej próbuj sam, nie jest to trudne: https://matematykaszkolna.pl/strona/1134.html

Bogdan: Sugeruję wyłączyć liczbę 6 przed nawias po prawej stronie równania.

Sławek: nie no chyba nie poradzę sobie...

Sławek: Ja niewymierność z mianownika umiem usunąć ale to chyba nie o to chodzi?

Sławek: pomoze ktosss?

Bogdan: Powtarzam − wyłącz liczbę 6 przed nawias po prawej stronie równania a²(6 + √3) = 36 + 6√3.

Sławek: a²(6+√3) = 36 + 6(√3) − tak ?

;): a²(6 + √3) = 6(6 + √3) Zauważ że masz 2 identyczne nawiasy to coś powinno się skrócić

Sławek: aha i wtedy wyjdzie, ze a² = 6, czyli, ze a = √6 ?

Sławek: bo wtedy by wychodziło, że V = a²√3 / 4 x a = 6√3/4 x √6 = 3√3/2 x √6 a tal być nie mozę. Bo w odpowiedziach jest, że V = 4,5√2

Godzio: A czemu tak być nie może ? √3 * √6 = √3 * √3 * √2 = 3√2

Sławek: bo w odpowiedzi w zbiorze zadań jest, ze to się równa 4,5√2