Planimetria (Okrąg w układzie współrzędnych) Maja: Bardzo proszę o pomoc w rozwiązaniu tego zadania: Wyznacz równanie okręgu o środku w punkcie (0;0), jeśli do tego okręgu należypunkt P. a) P(−3,0) Może się przyda: Okrąg o środku w początku układu współrzędnych i promieniu r jest zbiorem wszystkich punktów płaszczyzny (x, y) spełniających równanie: x²+y²=r² lub: Okrąg o środku w punkcie (a, b) i promieniu r jest zbiorem wszystkich punktów płaszczyzny (x, y) spełniających równanie : (x−a)²+(y−b)²=r². Byłabym wdzieczna za rozwiązanie tego przykładu.

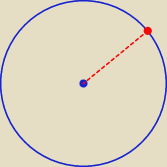
Bogdan: Czym jest odcinek łączący środek okręgu z punktem leżącym na okręgu?

Maja: Noo... promieniem.

Bogdan: Tak, jaki stąd wniosek?

Bogdan: Podpowiedź: jeśli dane są dwa punkty: A(x₁, y₁) i B(x₂, y₂), to jak można wyznaczyć długość odcinka AB ?

Maja: Ja myślałam, żeby podstawić −3 pod x, 0 pod y =r, ale to by nie miało sensu...

Maja: No to wtedy można by było wykorzystać taki wzór: |AB|=√(x2−x1)²+(y2−y1)². Z tym, że te2 i 1 w dolnych indeksach.

Bogdan: Jeśli okrąg o środku w punkcie O(0, 0) ma równanie: x² + y² = r², to zapis ten oznacza, że każdy punkt leżący na okręgu spełnia to równanie. Twój pomysł ma w tym przypadku sens.

Bogdan: |AB|² = (x₂ − x₁)² + (y₂ − y₁)² Jeśli x₁ = 0 i y₁ = 0, to |AB|² = x₂² + y₂² Niech r = |AB|, wtedy r² = x₂² + y₂²

krystek: Maja i ten wzór miałas wykorzystać bo r=IABI

Maja: No i załóżmy, że gdybym wykorzystała to: r²= x2² + y2² i podstwiła, to wydzie coś takiego chyba : r²=(−3)² + 0² r²=9 r=3 I o ile dobrze to zrobiłam, to nie wiem, jaki sens miało by rozwiązywanie czegoś takiego, skoro w poleceniu chodzi o wyznaczenie równania okręgu. Sorry, ze tak ciężko kapuję, ale nie przerabiałam jeszcze tego tematu, a potrzebuję rozwiązanie.

krystek: sama napisałaś jak wygląda równanie okręgu osrodku w p(o,o) i potrzebny jest Tobie promień.Pomyśl! (x−0)²+(y−0)²=r²

Maja: To jest głupie.

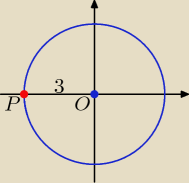
Bogdan: Zadanie jest banalne i nie wymagało obliczeń. Jeśli punkt P(−3, 0) leży na okręgu x² + y² = r², to r = |OP| = 3 i równanie okręgu ma wzór x² + y² = 9

Patrycja: Ano faktycznie banalne... No i trzeba było tak od razu. Dziękuję.