geometria ^^: 1.Uzasadnij, ze pole czworokąta opisanego na okręgu o promieniu r jest równe r(a+b) , gdzie a i b są długościami dwóch przeciwległych boków. 2. Wskaż, że stosunek obwodu koła do obwodu wielokąta opisanego na nim jest równy stosunkowi pola koła do pola wielokąta. 3. Na okręgu opisano trapez równoramienny o obwdzie p. Jaka jest odległość między środkami jego ramion?

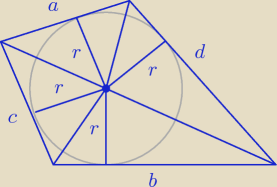
Godzio: Z własności wpisania okręgu w czworokąt mamy: a + b = c + d

	1		1		1		1		1
P =		cr +		br +		ar +		dr =		r(a + b + c + d) =
	2		2		2		2		2

	1
=		r(a + b + a + b) = r(a + b)
	2

Godzio: Teza:

Lk		Pk
	=
Lw		Pw

Lk		2πr
	=
Lw		a + b + c + d + ...

Pk		πr2		2πr2
	=		=
Pw		1   (ar + br + cr + dr + ... 2		r(a + b + c + d + ...

	2πr		Lk
=		=
	a + b + c + d + ...		Lw

Godzio: Z warunku wpisania okręgu w czworokąt: a + b = 2c

	a + b		1
L = a + b + 2c = p ⇒ 2(a + b) = p ⇒		=		p
	2		4

	1
x =		p
	4